How to Calculate the Area of a Triangle

Using the Base and Height

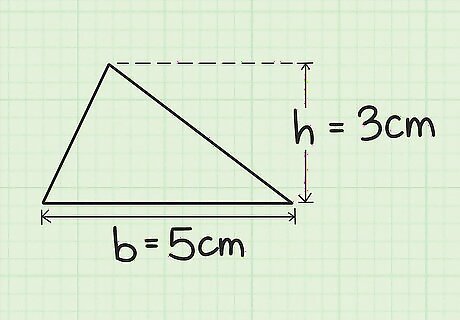
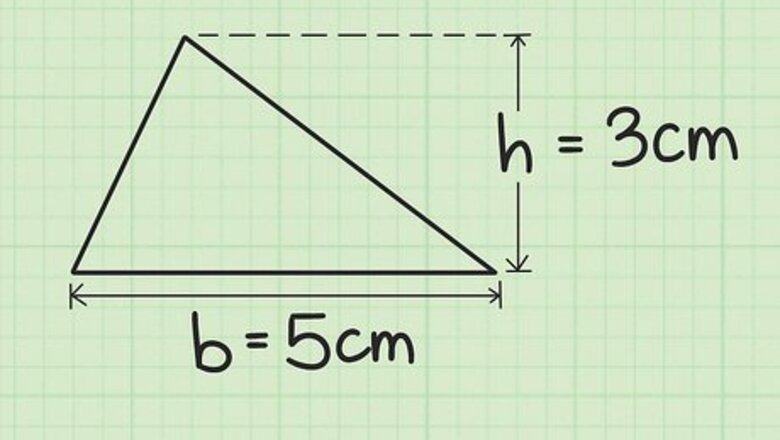
Find the base and height of the triangle. The base is one side of the triangle. The height is the measure of the tallest point on a triangle. It is found by drawing a perpendicular line from the base to the opposite vertex. This information should be given to you, or you should be able to measure the lengths. For example, you might have a triangle with a base measuring 5 cm long, and a height measuring 3 cm long.

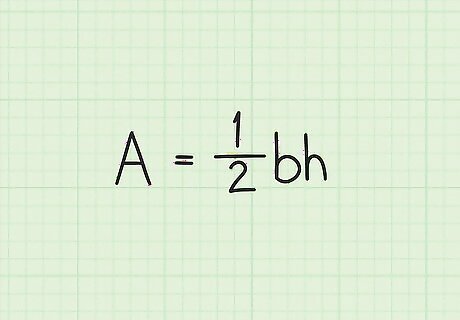
Set up the formula for the area of a triangle. The formula is Area = 1 2 ( b h ) {\displaystyle {\text{Area}}={\frac {1}{2}}(bh)} {\text{Area}}={\frac {1}{2}}(bh), where b {\displaystyle b} b is the length of the triangle’s base, and h {\displaystyle h} h is the height of the triangle.

Plug the base and height into the formula. Multiply the two values together, then multiply their product by 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}. This will give you the area of the triangle in square units. For example, if the base of your triangle is 5 cm and the height is 3 cm, you would calculate: Area = 1 2 ( b h ) {\displaystyle {\text{Area}}={\frac {1}{2}}(bh)} {\text{Area}}={\frac {1}{2}}(bh) Area = 1 2 ( 5 ) ( 3 ) {\displaystyle {\text{Area}}={\frac {1}{2}}(5)(3)} {\text{Area}}={\frac {1}{2}}(5)(3) Area = 1 2 ( 15 ) {\displaystyle {\text{Area}}={\frac {1}{2}}(15)} {\text{Area}}={\frac {1}{2}}(15) Area = 7.5 {\displaystyle {\text{Area}}=7.5} {\text{Area}}=7.5 So, the area of a triangle with a base of 5 cm and a height of 3 cm is 7.5 square centimeters.

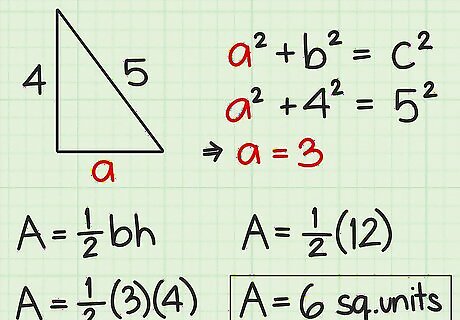
Find the area of a right triangle. Since two sides of a right triangle are perpendicular, one of the perpendicular sides will be the height of the triangle. The other side will be the base. So, even if the height and/or base is unstated, you are given them if you know the side lengths. Thus you can use the Area = 1 2 ( b h ) {\displaystyle {\text{Area}}={\frac {1}{2}}(bh)} {\text{Area}}={\frac {1}{2}}(bh) formula to find the area. You can also use this formula if you know one side length, plus the length of the hypotenuse. The hypotenuse is the longest side of a right triangle and is opposite the right angle. Remember that you can find a missing side length of a right triangle using the Pythagorean Theorem ( a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{{2}}+b^{{2}}=c^{{2}}). For example, if the hypotenuse of a triangle is side c, the height and base would be the other two sides (a and b). If you know that the hypotenuse is 5 cm, and the base is 4 cm, use the Pythagorean theorem to find the height: a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{{2}}+b^{{2}}=c^{{2}} a 2 + 4 2 = 5 2 {\displaystyle a^{2}+4^{2}=5^{2}} a^{{2}}+4^{{2}}=5^{{2}} a 2 + 16 = 25 {\displaystyle a^{2}+16=25} a^{{2}}+16=25 a 2 + 16 − 16 = 25 − 16 {\displaystyle a^{2}+16-16=25-16} a^{{2}}+16-16=25-16 a 2 = 9 {\displaystyle a^{2}=9} a^{{2}}=9 a = 3 {\displaystyle a=3} a=3Now, you can plug the two perpendicular sides (a and b) into the area formula, substituting for the base and height: Area = 1 2 ( b h ) {\displaystyle {\text{Area}}={\frac {1}{2}}(bh)} {\text{Area}}={\frac {1}{2}}(bh) Area = 1 2 ( 4 ) ( 3 ) {\displaystyle {\text{Area}}={\frac {1}{2}}(4)(3)} {\text{Area}}={\frac {1}{2}}(4)(3) Area = 1 2 ( 12 ) {\displaystyle {\text{Area}}={\frac {1}{2}}(12)} {\text{Area}}={\frac {1}{2}}(12) Area = 6 {\displaystyle {\text{Area}}=6} {\text{Area}}=6 EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Use this visual trick to understand the Pythagorean Theorem. Imagine a right triangle with squares constructed on each leg and the hypotenuse. by rearranging the smaller squares within the larger square, the areas of the smaller squares (a² and b²) will add up visually to the area of the larger square (c²).

Using Side Lengths

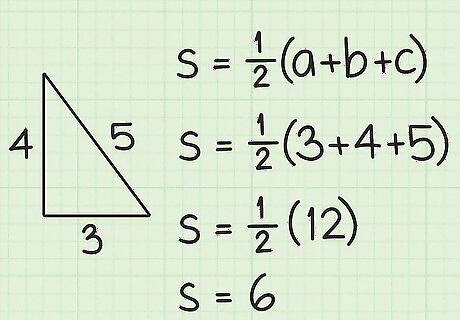
Calculate the semiperimeter of the triangle. The semi-perimeter of a figure is equal to half its perimeter. To find the semiperimeter, first calculate the perimeter of a triangle by adding up the length of its three sides. Then, multiply by 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}. For example, if a triangle has three sides that are 5 cm, 4 cm, and 3 cm long, the semiperimeter is shown by: s = 1 2 ( 3 + 4 + 5 ) {\displaystyle s={\frac {1}{2}}(3+4+5)} s={\frac {1}{2}}(3+4+5) s = 1 2 ( 12 ) = 6 {\displaystyle s={\frac {1}{2}}(12)=6} s={\frac {1}{2}}(12)=6

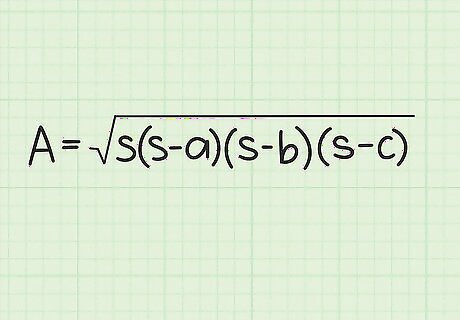
Set up Heron’s formula. The formula is Area = s ( s − a ) ( s − b ) ( s − c ) {\displaystyle {\text{Area}}={\sqrt {s(s-a)(s-b)(s-c)}}} {\text{Area}}={\sqrt {s(s-a)(s-b)(s-c)}}, where s {\displaystyle s} s is the semiperimeter of the triangle, and a {\displaystyle a} a, b {\displaystyle b} b, and c {\displaystyle c} c are the side lengths of the triangle.

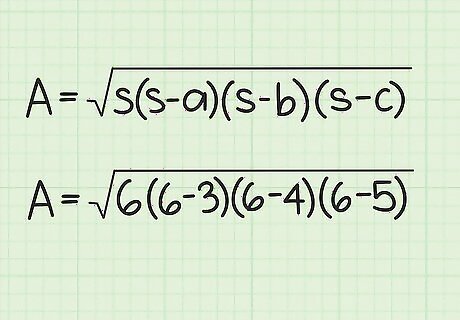
Plug the semiperimeter and side lengths into the formula. Make sure you substitute the semiperimeter for each instance of s {\displaystyle s} s in the formula. For example: Area = s ( s − a ) ( s − b ) ( s − c ) {\displaystyle {\text{Area}}={\sqrt {s(s-a)(s-b)(s-c)}}} {\text{Area}}={\sqrt {s(s-a)(s-b)(s-c)}} Area = 6 ( 6 − 3 ) ( 6 − 4 ) ( 6 − 5 ) {\displaystyle {\text{Area}}={\sqrt {6(6-3)(6-4)(6-5)}}} {\text{Area}}={\sqrt {6(6-3)(6-4)(6-5)}}

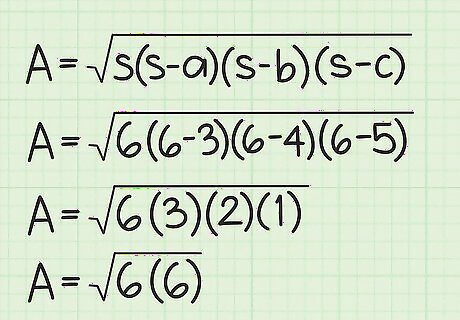
Calculate the values in parentheses. Subtract the length of each side from the semiperimeter. Then, multiply these three values together. For example: Area = 6 ( 6 − 3 ) ( 6 − 4 ) ( 6 − 5 ) {\displaystyle {\text{Area}}={\sqrt {6(6-3)(6-4)(6-5)}}} {\text{Area}}={\sqrt {6(6-3)(6-4)(6-5)}} Area = 6 ( 3 ) ( 2 ) ( 1 ) {\displaystyle {\text{Area}}={\sqrt {6(3)(2)(1)}}} {\text{Area}}={\sqrt {6(3)(2)(1)}} Area = 6 ( 6 ) {\displaystyle {\text{Area}}={\sqrt {6(6)}}} {\text{Area}}={\sqrt {6(6)}}

Multiply the two values under the radical sign. Then, find their square root. This will give you the area of the triangle in square units. For example: Area = 6 ( 6 ) {\displaystyle {\text{Area}}={\sqrt {6(6)}}} {\text{Area}}={\sqrt {6(6)}} Area = 36 {\displaystyle {\text{Area}}={\sqrt {36}}} {\text{Area}}={\sqrt {36}} Area = 6 {\displaystyle {\text{Area}}=6} {\text{Area}}=6So, the area of the triangle is 6 square centimeters.

Using One Side of an Equilateral Triangle

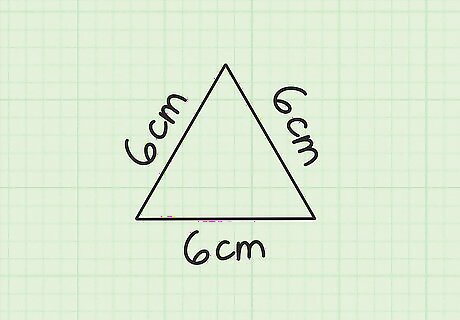
Find the length of one side of the triangle. An equilateral triangle has three equal side lengths and three equal angle measurements, so if you know the length of one side, you know the length of all three sides. For example, you might have a triangle with three sides that are 6 cm long.

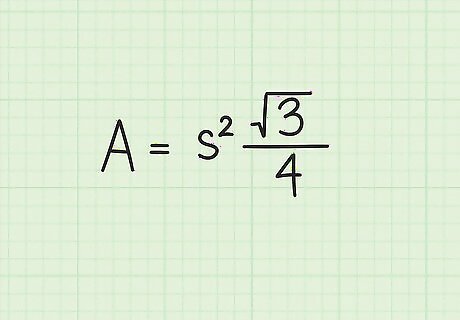
Set up the formula for the area of an equilateral triangle. The formula is Area = ( s 2 ) 3 4 {\displaystyle {\text{Area}}=(s^{2}){\frac {\sqrt {3}}{4}}} {\text{Area}}=(s^{{2}}){\frac {{\sqrt {3}}}{4}}, where s {\displaystyle s} s equals the length of one side of the equilateral triangle.

Plug the side length into the formula. Make sure you substitute for the variable s {\displaystyle s} s, and then square the value. For example if the equilateral triangle has sides that are 6 cm long, you would calculate: Area = ( s 2 ) 3 4 {\displaystyle {\text{Area}}=(s^{2}){\frac {\sqrt {3}}{4}}} {\text{Area}}=(s^{{2}}){\frac {{\sqrt {3}}}{4}} Area = ( 6 2 ) 3 4 {\displaystyle {\text{Area}}=(6^{2}){\frac {\sqrt {3}}{4}}} {\text{Area}}=(6^{{2}}){\frac {{\sqrt {3}}}{4}} Area = ( 36 ) 3 4 {\displaystyle {\text{Area}}=(36){\frac {\sqrt {3}}{4}}} {\text{Area}}=(36){\frac {{\sqrt {3}}}{4}}

Multiply the square by 3 {\displaystyle {\sqrt {3}}} {\sqrt {3}}. It’s best to use the square root function on your calculator for a more precise answer. Otherwise, you can use 1.732 for the rounded value of 3 {\displaystyle {\sqrt {3}}} {\sqrt {3}}. For example: Area = ( 36 ) 3 4 {\displaystyle {\text{Area}}=(36){\frac {\sqrt {3}}{4}}} {\text{Area}}=(36){\frac {{\sqrt {3}}}{4}} Area = 62.352 4 {\displaystyle {\text{Area}}={\frac {62.352}{4}}} {\text{Area}}={\frac {62.352}{4}}

Divide the product by 4. This will give you the area of the triangle in square units. For example: Area = 62.352 4 {\displaystyle {\text{Area}}={\frac {62.352}{4}}} {\text{Area}}={\frac {62.352}{4}} Area = 15.588 {\displaystyle {\text{Area}}=15.588} {\text{Area}}=15.588So, the area of an equilateral triangle with sides 6 cm long is about 15.59 square centimeters.

Using Trigonometry

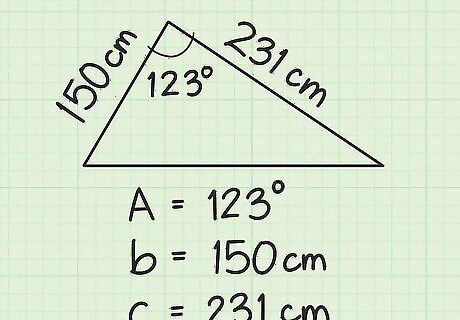
Find the length of two adjacent sides and the included angle. Adjacent sides are two sides of a triangle that meet at a vertex. The included angle is the angle between these two sides. For example, you might have a triangle with two adjacent sides measuring 150 cm and 231 cm in length. The angle between them is 123 degrees.

Set up the trigonometry formula for the area of a triangle. The formula is Area = b c 2 sin ⁡ A {\displaystyle {\text{Area}}={\frac {bc}{2}}\sin A} {\text{Area}}={\frac {bc}{2}}\sin A, where b {\displaystyle b} b and c {\displaystyle c} c are the adjacent sides of the triangle, and A {\displaystyle A} A is the angle between them.

Plug the side lengths into the formula. Make sure you substitute for the variables b {\displaystyle b} b and c {\displaystyle c} c. Multiply their values, then divide by 2. For example: Area = b c 2 sin ⁡ A {\displaystyle {\text{Area}}={\frac {bc}{2}}\sin A} {\text{Area}}={\frac {bc}{2}}\sin A Area = ( 150 ) ( 231 ) 2 sin ⁡ A {\displaystyle {\text{Area}}={\frac {(150)(231)}{2}}\sin A} {\text{Area}}={\frac {(150)(231)}{2}}\sin A Area = ( 34 , 650 ) 2 sin ⁡ A {\displaystyle {\text{Area}}={\frac {(34,650)}{2}}\sin A} {\text{Area}}={\frac {(34,650)}{2}}\sin A Area = 17 , 325 sin ⁡ A {\displaystyle {\text{Area}}=17,325\sin A} {\text{Area}}=17,325\sin A

Plug the sine of the angle into the formula. You can find the sine using a scientific calculator by typing in the angle measurement then hitting the “SIN” button. For example, the sine of a 123-degree angle is .83867, so the formula will look like this: Area = 17 , 325 sin ⁡ A {\displaystyle {\text{Area}}=17,325\sin A} {\text{Area}}=17,325\sin A Area = 17 , 325 ( .83867 ) {\displaystyle {\text{Area}}=17,325(.83867)} {\text{Area}}=17,325(.83867)

Multiply the two values. This will give you the area of the triangle in square units. For example: Area = 17 , 325 ( .83867 ) {\displaystyle {\text{Area}}=17,325(.83867)} {\text{Area}}=17,325(.83867) Area = 14 , 529.96 {\displaystyle {\text{Area}}=14,529.96} {\text{Area}}=14,529.96.So, the area of the triangle is about 14,530 square centimeters.