views
The Tutorial
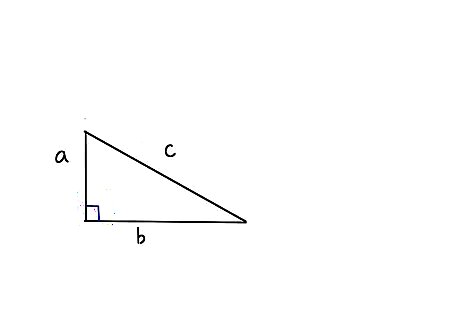
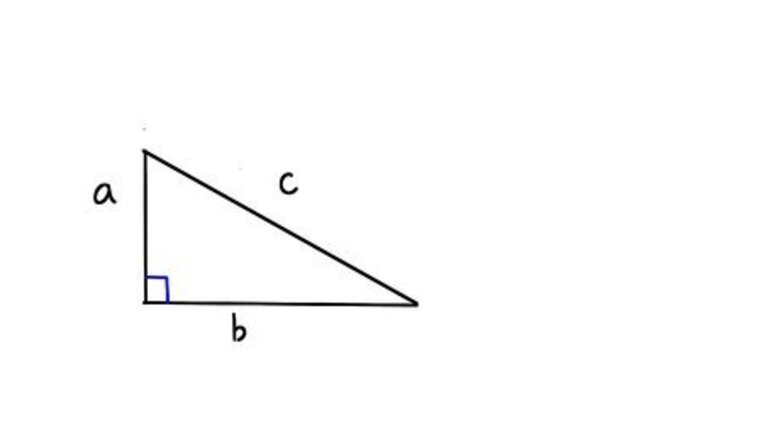
Construct a right triangle resting on side b with right angle to the left connected to upright and perpendicular side a, with side c connecting the endpoints of a and b.,br>
Construct a similar triangle with side b now extending in a straight line from the original side a, then with side a parallel along the top to the bottom original side b, and side c connecting the endpoints of the new a and b.
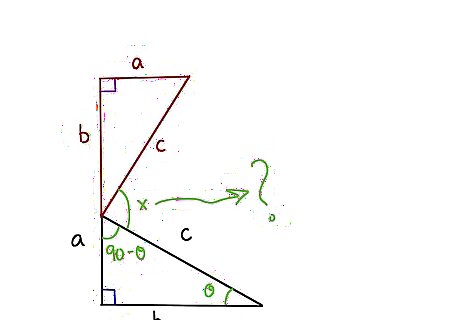
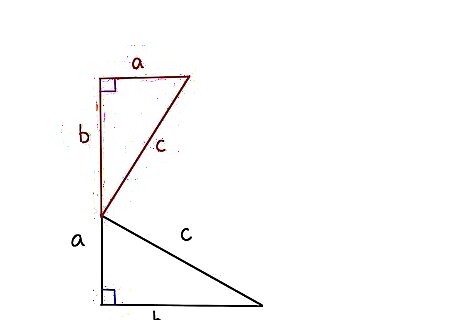
Understand the goal. We are interested to know the angle x formed where the two side c's meet. Thinking about it, the original triangle was made of 180 degrees with the angle on the right at the far end of b, called theta, and the other angle at the top of a, being 90 degrees minus theta, as all the angles total 180 degrees and we already have one 90 degree angle.
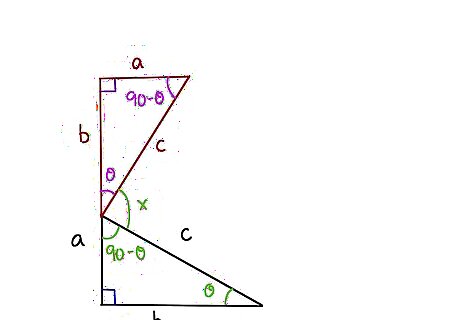
Transfer your angle knowledge to the upper new triangle. At the bottom, we have theta, at the top left we have 90 degrees, and the top right we have 90 degrees minus theta. The mystery angle x is 180 degrees. So theta + 90 degrees-theta + x = 180 degrees. Adding theta and negative theta gives us zero on the left, and subtracting 90 degrees from both sides leaves x equal to 90 degrees. So we have established that the mystery angle x = 90 degrees.Do Garfield's Proof of the Pythagorean Theorem Step 4Bullet1.jpg
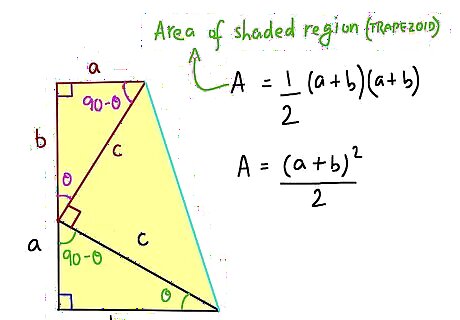
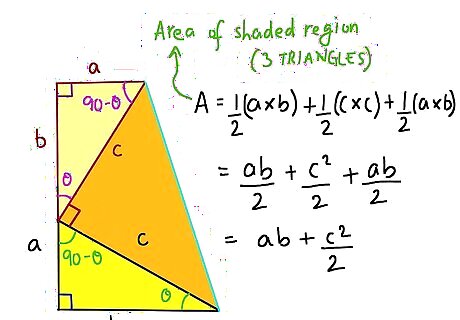
Look at the whole figure as a trapezoid in two ways. First, the formula for a trapezoid is A= the Height x (Base1 + Base 2)/2. The height is a+b and (Base1 + Base 2)/2 = 1/2(a + b). So that all equals 1/2 (a+b)^2.
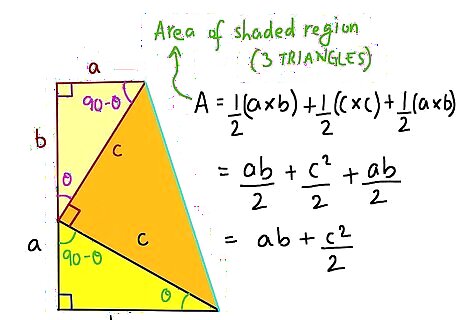
Look at the interior of the trapezoid and add up the areas, in order to set them equal to the formula just found. We have the two smaller triangles at bottom and left, and those together equal 2*1/2(a*b), which just equals (a*b). Then we also have 1/2 c*c, or 1/2 c^2. So together we have the other formula for the area of the trapezoid equaling (a*b)+ 1/2 c^2.
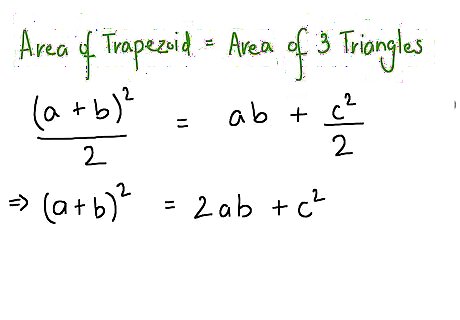
Set the two Area formulas equal. 1/2(a+b)^2=(a*b)+1/2 c^2. Now multiply both sides by 2 to get rid of the 1/2's 2(1/2 (a+b)^2) = 2((a*b)+ 1/2 c^2.) which simplifies as (a+b)^2 = 2ab + c^2. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Learning different proofs will help you master the Pythagorean Theorem. Discovering the Pythagorean Theorem can be approached through visual or algebraic methods. By exploring the proof from different angles, you can solidify your knowledge and make it easier to remember.
Explanatory Charts, Diagrams, Photos

Now expand the left hand square, which becomes a^2 + 2ab + b^2, and we see we can subtract 2ab from both sides of a^2 + 2ab + b^2, = 2ab + c^2. to obtain a^2 + b^2 = c^2, The Pythagorean Theorem!
Finished!




















Comments
0 comment