How to Find the Distance Between Two Points

• Jot down the coordinates that you're measuring the distance between.
• Plug these coordinates into the distance formula: ${\displaystyle {\sqrt {(}}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})}$.
• Solve the formula by squaring the differences of the x and y values, adding these differences together, and finding the square root of the remaining sum.

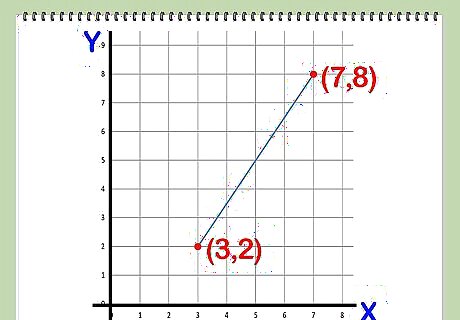
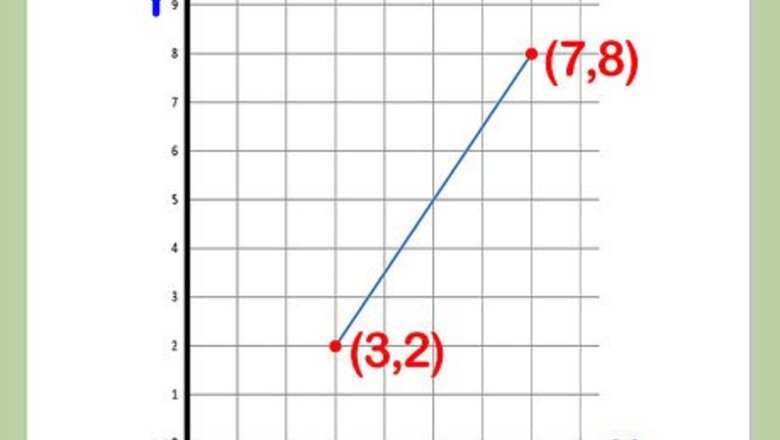
Take the coordinates of two points you want to find the distance between. Call one point Point 1 (x1,y1) and make the other Point 2 (x2,y2). It does not terribly matter which point is which, as long as you keep the labels (1 and 2) consistent throughout the problem. x1 is the horizontal coordinate (along the x axis) of Point 1, and x2 is the horizontal coordinate of Point 2. y1 is the vertical coordinate (along the y axis) of Point 1, and y2 is the vertical coordinate of Point 2. For an example, take the points (3,2) and (7,8). If (3,2) is (x1,y1), then (7,8) is (x2,y2).

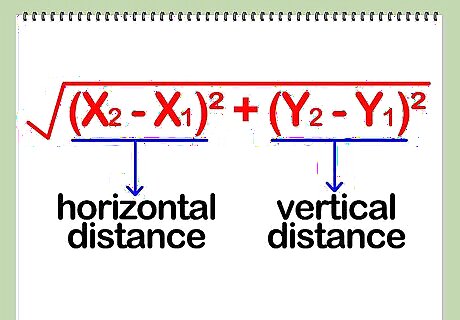
Know the distance formula. This formula finds the length of a line that stretches between two points: Point 1 and Point 2. The linear distance is the square root of the square of the horizontal distance plus the square of the vertical distance between two points. More simply put, it is the square root of: ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 {\displaystyle (x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}} (x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}

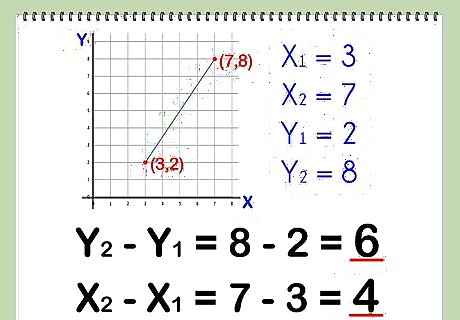
Find the horizontal and vertical distance between the points. First, subtract y2 - y1 to find the vertical distance. Then, subtract x2 - x1 to find the horizontal distance. Don't worry if the subtraction yields negative numbers. The next step is to square these values, and squaring always results in a positive number. Find the distance along the y-axis. For the example points (3,2) and (7,8), in which (3,2) is Point 1 and (7,8) is Point 2: (y2 - y1) = 8 - 2 = 6. This means that there are six units of distance on the y-axis between these two points. Find the distance along the x-axis. For the same example points (3,2) and (7,8): (x2 - x1) = 7 - 3 = 4. This means that there are four units of distance separating the two points on the x-axis.

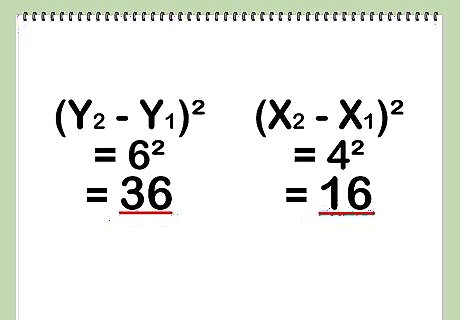
Square both values. This means that you will square the x-axis distance (x2 - x1), and that you will separately square the y-axis distance (y2 - y1). 6 2 = 36 {\displaystyle 6^{2}=36} 6^{2}=36 4 2 = 16 {\displaystyle 4^{2}=16} 4^{2}=16

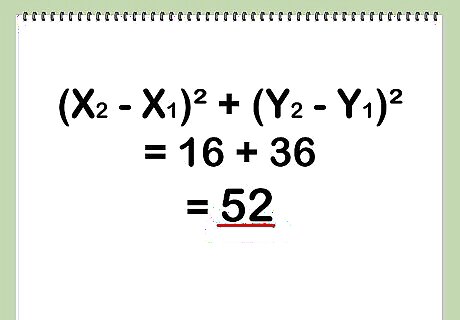
Add the squared values together. This will give you the square of the diagonal, linear distance between your two points. In the example of the points (3,2) and (7,8), the square of (8 - 2) is 36, and the square of (7 - 3) is 16. 36 + 16 = 52.

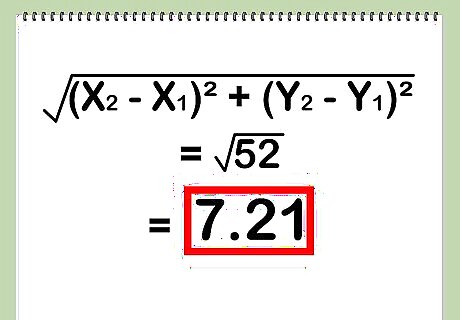
Take the square root of the equation. This is the final step in the equation. The linear distance between the two points is the square root of the sum of the squared values of the x-axis distance and the y-axis distance. To carry on the example: the distance between (3,2) and (7,8) is sqrt (52), or approximately 7.21 units.