views
(
x
3
,
y
3
)
=
(
x
1
+
x
2
2
,
y
1
+
y
2
2
)
{\displaystyle (x_{3},y_{3})=({\frac {x_{1}+x_{2}}{2}},{\frac {y_{1}+y_{2}}{2}})}
. In this article, the midpoint (
x
3
,
y
3
{\displaystyle x_{3},y_{3}}
)
=
{\displaystyle =}
(
−
6
,
−
2
)
{\displaystyle (-6,-2)}
and the given endpoint (
x
1
,
y
1
{\displaystyle x_{1},y_{1}}
)
=
{\displaystyle =}
(
−
3
,
−
5
)
{\displaystyle (-3,-5)}
are used as examples. The rest is algebra: isolate
x
2
{\displaystyle x_{2}}
and
y
2
{\displaystyle y_{2}}
(separately) to find the second endpoint coordinates.
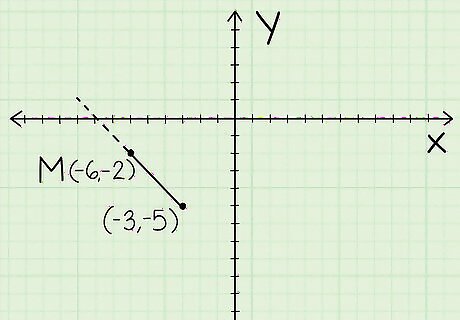
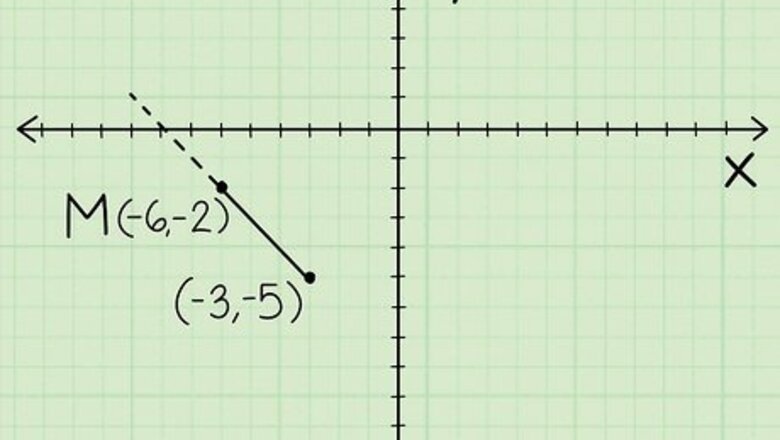
Graph your values (optional). This will allow you to get a visual understanding of the linear equation. Make sure that you label your midpoint, M {\displaystyle M} M.
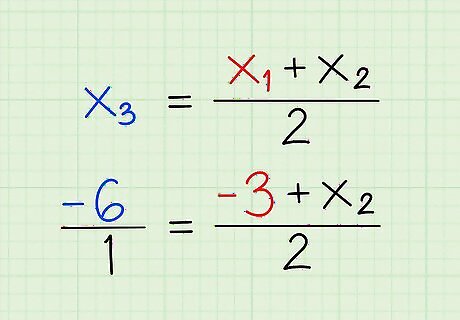
Rewrite the x coordinate formula, substituting x 1 {\displaystyle x_{1}} x_{1} and x 3 {\displaystyle x_{3}} x_{3}. For example: − 3 + x 2 2 = − 6 1 {\displaystyle {\frac {-3+x_{2}}{2}}={\frac {-6}{1}}} {\frac {-3+x_{{2}}}{2}}={\frac {-6}{1}}. − 6 = − 6 1 {\displaystyle -6={\frac {-6}{1}}} -6={\frac {-6}{1}} because they mean the same thing. It's easier to solve when both sides are fractions initially.
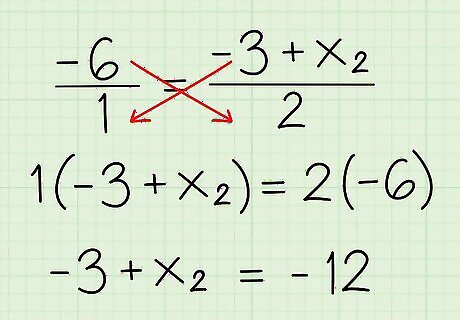
Cross multiply to eliminate the denominators. Multiply the top-left and bottom-right side: ( x 1 + x 2 ) × = 2 {\displaystyle (x_{1}+x_{2})\times =2} (x_{1}+x_{2})\times =2. Repeat with the top-right value by the bottom right value ( x 3 {\displaystyle x_{3}} x_{{3}} and 2 {\displaystyle 2} 2). For example: You start with: − 3 + x 2 2 = − 6 1 {\displaystyle {\frac {-3+x_{2}}{2}}={\frac {-6}{1}}} {\frac {-3+x_{{2}}}{2}}={\frac {-6}{1}} Multiply the top-left and bottom-right: ( − 3 + x 2 ) × 1 = − 3 + x 2 {\displaystyle (-3+x_{2})\times 1=-3+x_{2}} (-3+x_{{2}})\times 1=-3+x_{{2}} Multiply the bottom-left and top-right (opposite of what was just done): 2 × − 6 = − 12 {\displaystyle 2\times -6=-12} 2\times -6=-12 The result is a simple algebraic equation: − 3 + x 2 = − 12 {\displaystyle -3+x_{2}=-12} -3+x_{{2}}=-12
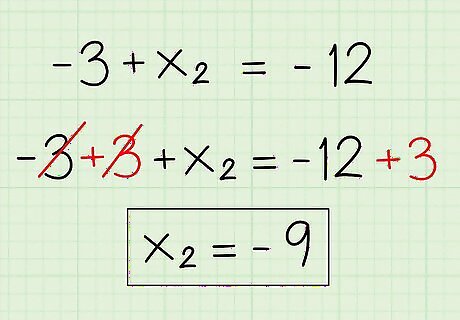
Solve the remaining algebraic equation including isolating the variable. Perform the inverse operation on the constant to isolate the variable—and do it to both sides! For example: Perform the inverse operation of − 3 {\displaystyle -3} -3 by adding + 3 {\displaystyle +3} +3 to the left side. This isolates the variable because the positive reverses the negative. However, you will need to add + 3 {\displaystyle +3} +3 to the other side of the equation (beyond the equals sign). − 3 + 3 + x 2 = − 12 + 3 {\displaystyle -3{\cancel {+3}}+x_{2}=-12+3} -3{\cancel {+3}}+x_{{2}}=-12+3 x 2 = − 9 {\displaystyle x_{2}=-9} x_{{2}}=-9. This means that the x {\displaystyle x} x value of the second endpoint you're trying to find, is − 9 {\displaystyle -9} -9.
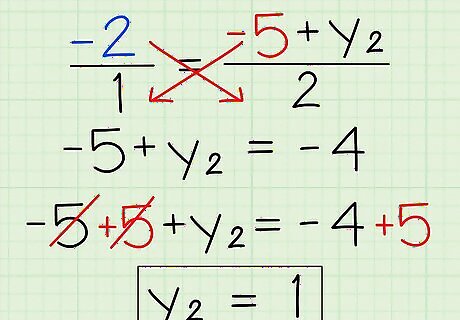
Repeat the process above, now solving for y {\displaystyle y} y instead. You've solved half of the problem by finding the x {\displaystyle x} x coordinate of the endpoint. Now, your endpoint is ( − 9 , y ) {\displaystyle (-9,y)} (-9,y). As you can see, you're not done! Here's how to solve for y {\displaystyle y} y: Substitute y 1 {\displaystyle y_{1}} y_{{1}} and y 3 {\displaystyle y_{3}} y_{{3}}: − 5 + y 2 2 = − 2 1 {\displaystyle {\frac {-5+y_{2}}{2}}={\frac {-2}{1}}} {\frac {-5+y_{{2}}}{2}}={\frac {-2}{1}} Cross multiply and isolate the variable: − 5 + 5 + y 2 = − 4 + 5 {\displaystyle -5{\cancel {+5}}+y_{2}=-4+5} -5{\cancel {+5}}+y_{{2}}=-4+5 Y coordinate: y 2 = 1 {\displaystyle y_{2}=1} y_{{2}}=1 Final answer (missing endpoint): ( − 9 , 1 ) {\displaystyle (-9,1)} (-9,1)



















Comments
0 comment