How to Calculate Sensitivity, Specificity, Positive Predictive Value, and Negative Predictive Value

Define a population to sample, e.g. 1000 patients in a clinic.

Define the disease or characteristic of interest, e.g. syphilis.

Have a well-established gold standard test to determine the prevalence of disease or characteristic, e.g. darkfield microscopic documentation of the presence of the Treponema pallidum bacteria from scrapes off a syphilitic sore, in collaboration with clinical findings. Use the gold standard test to determine who has the character and who does not. For illustration, let us say 100 people have it and 900 do not.

Have a test that you are interested in determining its sensitivity, specificity, positive predictive value, and negative predictive value for this population, and run this test on everyone within the chosen population sample. For example, let this test be a rapid plasma reagin (RPR) test to screen for syphilis. Use it to test the 1000 people in the sample.

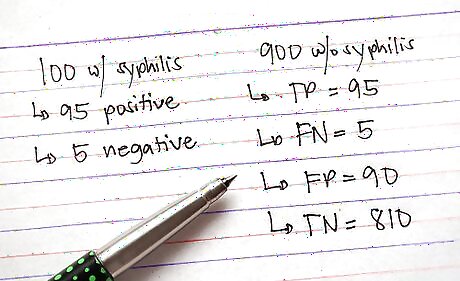
For people that have the characteristic (as determined by the gold standard), record the number of people who tested positive and the number of people who tested negative. Do the same for people that do not have the characteristic (as determined by the gold standard). You will end up with four numbers. People with the characteristic AND tested positive are the true positives (TP). People with the characteristic AND tested negative are the false negatives (FN). People without the characteristic AND tested positive are the false positives (FP). People without the characteristic AND tested negative are the true negatives (TN) For example, let us suppose you did the RPR test on the 1000 patients. Among the 100 patients with syphilis, 95 of them tested positive, and 5 tested negative. Among the 900 patients without syphilis, 90 tested positive, and 810 tested negative. In this case, TP=95, FN=5, FP=90, and TN=810.

To calculate the sensitivity, divide TP by (TP+FN). In the case above, that would be 95/(95+5)= 95%. The sensitivity tells us how likely the test is to come back positive in someone who has the characteristic. Among all people that have the characteristic, what proportion will test positive? 95% sensitivity is pretty good.

To calculate the specificity, divide TN by (FP+TN). In the case above, that would be 810/(90+810)= 90%. The specificity tells us how likely the test is to come back negative in someone who does not have the characteristic. Among all people without the characteristic, what proportion will test negative? 90% of specificity is pretty good.

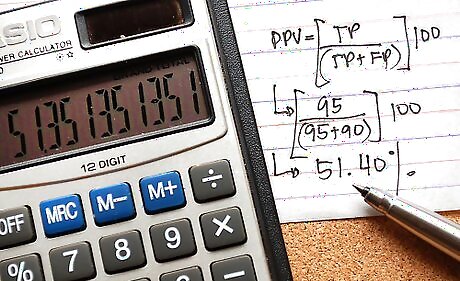
To calculate the positive predictive value (PPV), divide TP by (TP+FP). In the case above, that would be 95/(95+90)= 51.4%. The positive predictive value tells us how likely someone is to have the characteristic if the test is positive. Among all people that test positive, what proportion truly has the characteristic? 51.4% PPV means that if you test positive, you have a 51.4% chance of actually having the disease.

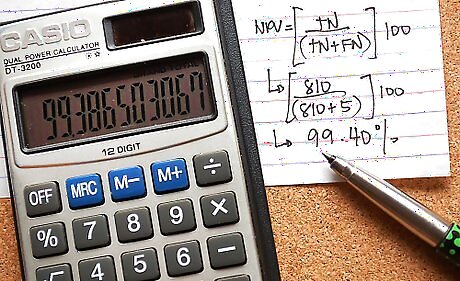
To calculate the negative predictive value (NPV), divide TN by (TN+FN). In the case above, that would be 810/(810+5)= 99.4%. The negative predictive value tells us how likely someone is to not have the characteristic if the test is negative. Among all people that test negative, what proportion truly does not have the characteristic? 99.4% NPV means that if you test negative, you have a 99.4% chance of not having a disease.