
views
Introducing the Basics

Know when to teach place value. If you are teaching within a pre-set curriculum, then you may already have an idea of how place value will fit into the larger scope of your course. If you are tutoring or homeschooling, you are likely working within a more flexible structure. Plan to teach place value shortly after students have learned to count by ones and perform simple addition and subtraction operations – generally around first or second grade. An understanding of place value will lay the foundation for these kids to dive into more complex mathematical concepts.

Introduce the concept of group counting. Most young students have only learned to count numbers by ones: one... two... three... four. This is sufficient for basic addition and subtraction, but it is too basic to give students a strong foundation for understanding more complex functions. Before you teach the kids how to break down large numbers into place values, it may be helpful to teach them how to chunk groups of small numbers together into big numbers. Teach your class how to skip-count by twos, threes, fives, and tens. This is an essential concept for students to understand before they learn place value. Especially try to establish a strong "sense of ten." Modern western mathematics uses the number ten as a base, so it will be much easier for kids to learn more complex systems if they are used to thinking in this way. Teach your pupils to group numbers instinctively into sets of ten.

Review the idea of place value. Give yourself a refresher. Make sure that you fully understand the concept yourself before you try to teach it to a group of young students. Place value, simply put, is the idea that the value of a digit (0-9) depends on its "place" or position in a number.

Explain the difference between numbers and digits. The digits are the basic ten number symbols that make up every number: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. We combine these digits to form every single other number. A digit can be a number (e.g. the number 7), but only if it is not grouped with another digit. When two or more digits are grouped together, the order of those digits form a larger number. Demonstrate that on their own, "1" is the number one and "7" is the number seven. When you put them together, as "17," they form the number seventeen. Similarly, "3" and 5" together make the number thirty-five. Draw several other examples to bring the point home.
Teaching with Visual Examples

Show the kids that it is easier to count in groups of ten. Use 30-40 small, countable, and fairly homogeneous objects: pebbles, marbles, or erasers. Scatter the objects on a table in front of your students. Explain that in modern math, we use the number 10 as a base. Arrange the objects into several groups of then, and count them for the class. Show the students that four groups of 10 pebbles equals 40.

Translate the pebble example into written numbers. Sketch out the concept on a whiteboard. First, draw a basic T-chart, Write the number 1 in the top-right corner of the T-chart. Then, write a 10 in the top-left compartment. Write a 0 in the (right-hand) column labeled "1," and write a 4 in the (left-hand) column labeled "10." Now, explain to the class that each number you made with the pebbles has its own "place."
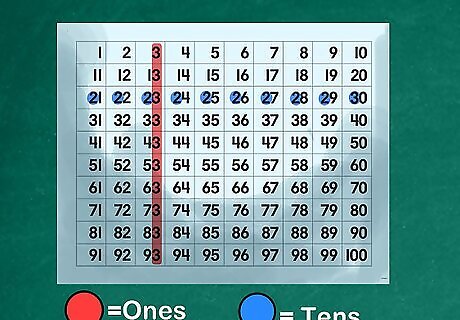
Use a number board to illustrate the basic place values. Make or print out a "number board" that lays out all of the numbers sequentially from 1-100. Show your students how the numbers from 0 to 9 interact with the numbers from 10 to 100. Explain that every number from 10 to 99 is really made up of two numbers, with one number in the "ones" place and a modifying number in the "tens" place. Show how the number "4" signifies "four" when it is in the "ones" place, but acts as a prefix for the set of "40" when it is located in the "tens" place. Illustrate the "ones" place. Direct the class mark or cover up every number that has a "3" in the "ones" place: 3, 13, 23, 33, 43, 53, 63, 73, 83, 93. Explain the "tens" place. Have the class point out every number with a "2" in the "tens" place: 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. Explain that the "3" in "23" is stacked on top of the "20" that is signified by the "2." Teach your kids to read the "tens" place as a trigger.

Experiment with other visual teaching tools. You can arrange physical objects or draw on a whiteboard. You can explain place value using increments of money, which students have likely already learned to associate with scaled numerical values. For a fun and interactive exercise, try using the students themselves as the "groups" of values. Memory is predominantly visual, and the concept of place value can be abstract until you put it into visual terms. For that matter, numerical symbols themselves can be abstract for young kids! Look for ways to frame group counting and place value so that they come across as simple, tangible, and intuitive. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Use playful academic activities and games to build students' math skills. Visual aids such as models, diagrams, and real-world objects transform abstract concepts into something more relatable, promoting a deeper understanding. Interactive activities enhance a student's learning by making math fun and engaging.

Use colors. Try using differently-colored chalks or markers to visually demonstrate place value. For instance, write out various numbers using a black marker for the "ones" place and a blue marker for the "tens." Thus, you would write the number 40 with a blue "4" and a black "0." Repeat this trick with a wide range of numbers to show that place value applies across the board.
Using an Interactive Example
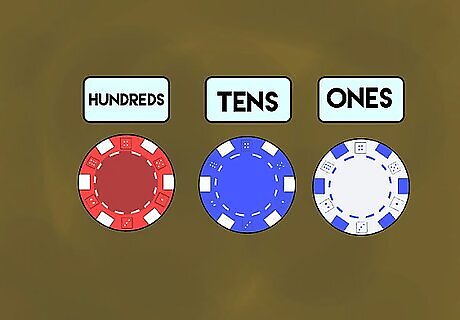
Teach with poker chips. First, distribute poker chips to each student. Tell the class that the white poker chips stand for the "ones" place, the blue chips stand for the "tens," and the red poker chips stand for the "hundreds." Then, show the class how to create numbers using place value with your chips. Give them a number (e.g. 7) and place a white chip on the right side of your work table. Say another number – for instance, 30. Lay down three blue chips to represent the 3 (in the "tens" place) and zero white chips to represent the 0 (in the "ones" place.) You don't strictly need to use poker chips. You can use almost set of objects to represent the three basic value "places," as long as each group (color of chips, etc.) is standard, homogeneous, and easy to recognize.
Have the class trade chips. This is a way to illustrate the way that lower place values make up higher place values. Once the students demonstrate a solid understanding of place value: teach your class how to trade the white "ones" chips for blue "tens" chips, and "tens" chips for red "hundreds" chips. Ask the class, "How many blue chips can I get if I trade 16 white chips? If I trade three blue chips, how many white chips can I get?"
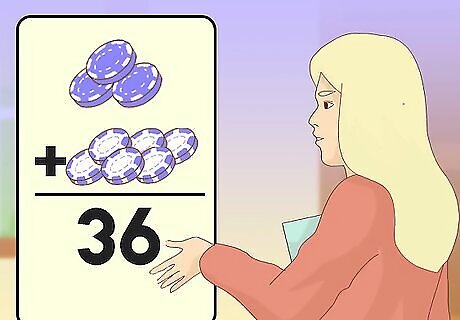
Demonstrate how to add and subtract with the poker chips. You should only approach this concept once the students have mastered the trading of poker chips. It may help to first draw the example of For a basic addition problem, direct your students to put three blue chips (tens) and six white chips (ones) together. Ask the class what number this makes. (It's 36!) Keep riffing off of the same number. Have your students add five white chips to their number 36. Ask your students what number they now have. (It's 41!) Then, take away one blue chip and ask the students what number they have. (It's 31!)



















Comments
0 comment