views
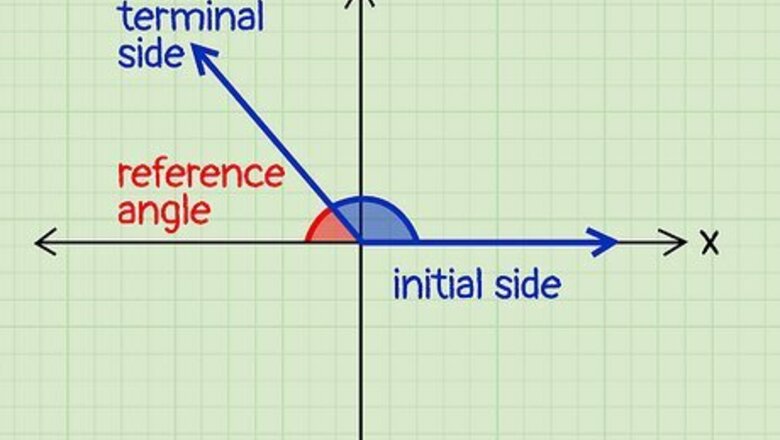
What is the reference angle?

The reference angle is made by the x-axis and terminal side of an angle. Every angle has an initial side, which is the ray that falls on the x-axis, and a terminal side, which is the angle’s other ray. The reference angle is the small angle formed by a given angle’s terminal side and the x-axis. Note: Reference angles are always positive and less than or equal to 90°. A ray is a straight line with 1 endpoint.
Calculating the Reference Angle
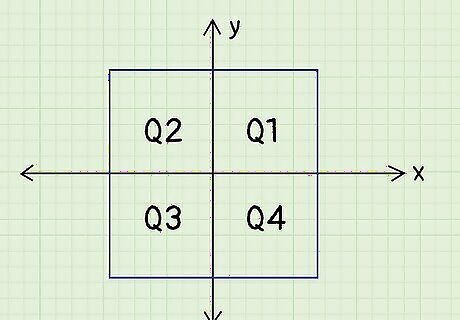
Determine what quadrant the given angle is in. The coordinate plane, or the intersection between the x-axis and y-axis, is split into 4 quadrants that span from 0° to 360° (or 0 to 2????, if the angle is in radians). Look at the angle given to you and determine which quadrant it lies in based on its value. Quadrant 1: Angles are between 0° to 90° or 0 to ????/2. Quadrant 2: Angles are between 90° to 180° or ????/2 to ????. Quadrant 3: Angles are between 180° to 270° or ???? to 3????/2. Quadrant 4: Angles are between 270° to 360° or 3????/2 to 2????. Memorize the unit circle to make finding the reference angle easier when it’s in radians.
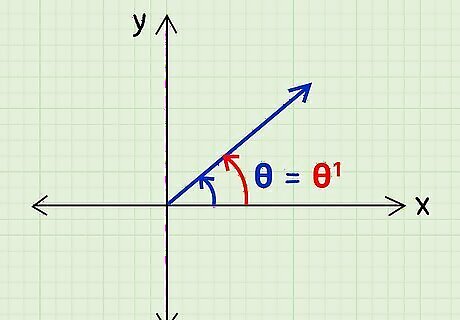
If the given angle is in quadrant 1, the reference angle is the same. When the angle given to you, θ {\displaystyle {\theta }} {\displaystyle {\theta }}, lies in the first quadrant, the reference angle, θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}}, is the same as the given angle. For example, find the reference angle θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} if your given angle is θ {\displaystyle {\theta }} {\displaystyle {\theta }} = 40°. 40° is in the first quadrant, so the reference angle θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} is also 40°.
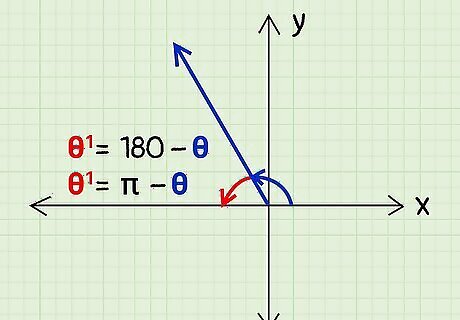
If the given angle is in quadrant 2, subtract the angle from 180°. When the angle given to you rests in the second quadrant, you subtract its value from 180° to get the reference angle, or θ 1 = 180 − θ {\displaystyle {\theta }^{1}=180-{\theta }} {\displaystyle {\theta }^{1}=180-{\theta }}. If the angle is in radians, subtract the angle from ????, or θ 1 = π − θ {\displaystyle {\theta }^{1}={\pi }-{\theta }} {\displaystyle {\theta }^{1}={\pi }-{\theta }}. For example, find the reference angle θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} if your given angle is θ {\displaystyle {\theta }} {\displaystyle {\theta }} = 120°. 120° is in the second quadrant. 180° - 120° = 60°. The reference angle is θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} = 60°.
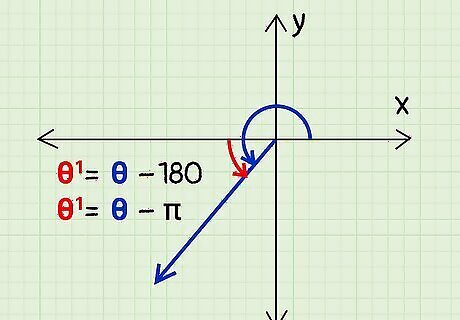
If the given angle is in quadrant 3, subtract 180° from the angle. When the angle given to you is in the third quadrant, you subtract 180° from the angle to get the reference angle, or θ 1 = θ − 180 {\displaystyle {\theta }^{1}={\theta }-180} {\displaystyle {\theta }^{1}={\theta }-180}. If the angle is in radians, subtract ???? from the angle, or θ 1 = θ − π {\displaystyle {\theta }^{1}={\theta }-{\pi }} {\displaystyle {\theta }^{1}={\theta }-{\pi }}. For example, find the reference angle θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} if your given angle is θ {\displaystyle {\theta }} {\displaystyle {\theta }} = 230°. 230° is in the third quadrant. 230° - 180° = 50°. The reference angle is θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} = 50°.
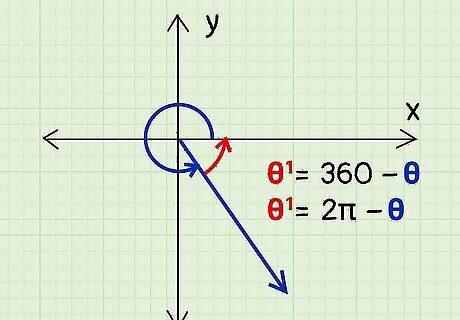
If the given angle is in quadrant 4, subtract the angle from 360°. When the angle given to you is in the fourth quadrant, subtract the angle from 360° to get the reference angle, or θ 1 = 360 − θ {\displaystyle {\theta }^{1}=360-{\theta }} {\displaystyle {\theta }^{1}=360-{\theta }}. If the angle is in radians, subtract the angle from 2????, or θ 1 = 2 π − θ {\displaystyle {\theta }^{1}=2{\pi }-{\theta }} {\displaystyle {\theta }^{1}=2{\pi }-{\theta }}. For example, find the reference angle θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} if your given angle is θ {\displaystyle {\theta }} {\displaystyle {\theta }} = 325°. 325° is in the fourth quadrant. 360° - 325° = 35°. The reference angle is θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} = 35°.
Finding the Reference Angle for Negative Angles & Angles Greater than 360° (2????)

Add or subtract 360° until the given angle is between 0° and 360°. Sometimes, you have to find the reference angle for a given angle that’s less than 0 or greater than 360° (if it’s in radians, less than 0 or greater than 2????). Finding the reference angle is still possible; you just first have to find its corresponding angle that’s between 0° and 360° (or between 0 and 2????, if the angle is in radians). If the angle is negative, keep adding 360° until it is between 0° and 360°. If the angle is in radians, keep adding 2???? until it is between 0 and 2????. If the angle is greater than 360°, keep subtracting 360° until it is between 0° and 360°. If the angle is in radians, subtract 2???? until it is between 0 and 2????. For example: If the given angle is -210°, add 360°. -210° + 360° = 150°. If the given angle is 545°, subtract 360°. 545° - 360° = 185°. If the given angle is -11????/6, add 2????. -11????/6 + 12????/6 = ????/6.
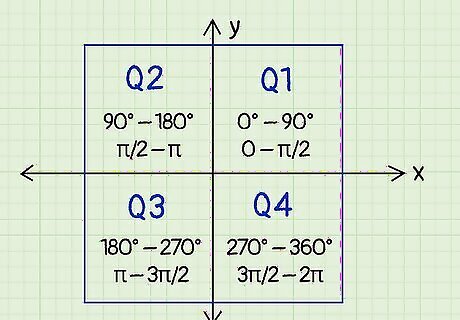
Determine which quadrant the new given angle is in. After adding or subtracting multiples of 360° (or 2????) from the given angle, find out where it now lies on the coordinate plane. Remember that: Angles between 0° to 90° or 0 to ????/2 are in quadrant 1. Angles between 90° to 180° or ????/2 to ???? are in quadrant 2. Angles between 180° to 270° or ???? to 3????/2 are in quadrant 3. Angles between 270° to 360° or 3????/2 to 2???? are in quadrant 4.
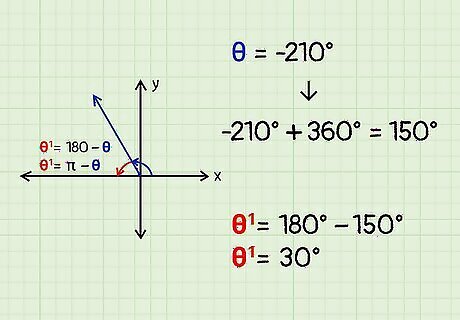
Find the reference angle based on the quadrant the given angle is in. Apply the formula to find the reference angle based on what quadrant the given angle is in. For example, find the reference angle θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} if your given angle is θ {\displaystyle {\theta }} {\displaystyle {\theta }} = -210°. Add 360°. -210° + 360° = 150°. 150° is in quadrant 2. To find the reference angle in quadrant 2, subtract the angle from 180°. 180° - 150° = 30°. The reference angle for θ {\displaystyle {\theta }} {\displaystyle {\theta }} = -210° is θ 1 {\displaystyle {\theta }^{1}} {\displaystyle {\theta }^{1}} = 30°.
Why is the reference angle useful?
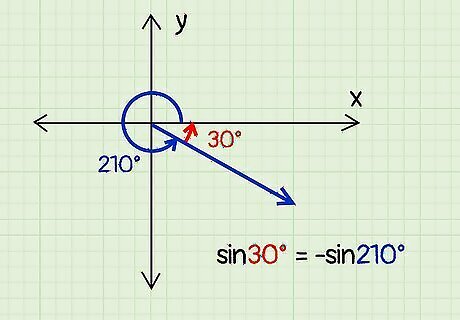
The trig function is the same for the given angle and reference angle. When finding the sine, cosine, tangent, or other trigonometric function of an angle, the value is the same for the given angle and the reference angle. This comes in handy when the given angle is an uncommon angle but the reference angle is an angle you already know the answer to, like 30° or 45°. For instance, you might be asked to find the value of sine 210°. You likely don’t know the answer off the top of your head, but you can easily determine that the reference angle of 210° is 30°. Sine 30° is ½, so sine 210° is -½. Note: The sine might be different for the given and reference angle. Each trig function is positive or negative, depending on the quadrant the angle is in: Quadrant 1: All functions are positive. Quadrant 2: Only sine is positive. Quadrant 3: Only tangent is positive. Quadrant 4: Only cosine is positive.



















Comments
0 comment