How Find the Weight of an Object Using Mass and Gravity

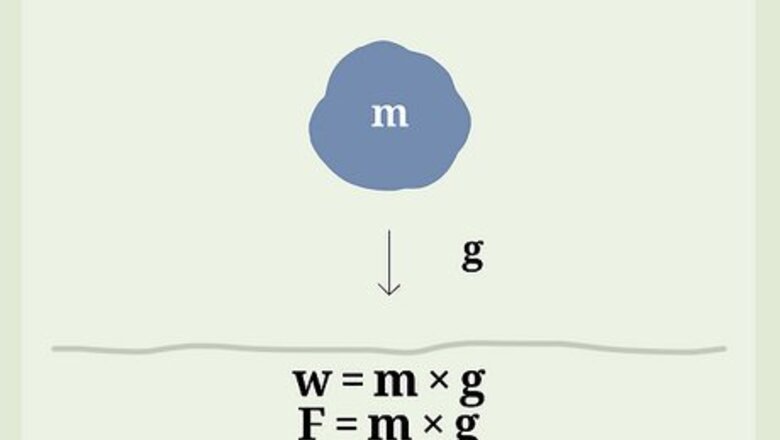
• The weight of an object equals the force of gravity exerted on that object. The mass of an object is always the same, but its weight changes depending on gravity.
• Use the formula ${\displaystyle w=m*g}$ to calculate weight from mass. In this formula, ${\displaystyle w}$ = weight (in N), ${\displaystyle m}$ = mass (in kg), and ${\displaystyle g}$ = acceleration due to gravity (in m/s²).
• Since weight is a force, scientists also write the equation as ${\displaystyle F=mg}$, where ${\displaystyle F}$ = force (in N), ${\displaystyle m}$ = mass (in kg), and ${\displaystyle g}$ = acceleration due to gravity (in m/s²).
• The value of gravity, ${\displaystyle g}$, is 9.8 m/s² on Earth. Its value is different elsewhere in the universe. For example, on the moon, ${\displaystyle g}$ = 1.622 m/s².

Calculating Weight

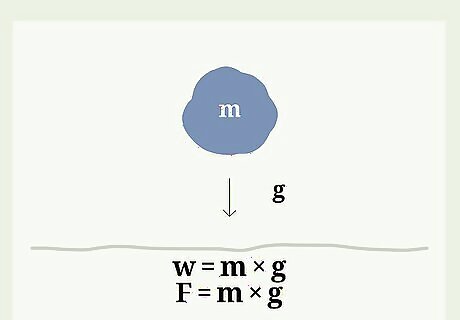
Use the formula w = m ∗ g {\displaystyle w=m*g} {\displaystyle w=m*g} to convert weight into mass. Weight is defined as the force of gravity on an object. Scientists put that sentence into an equation by writing w = m ∗ g {\displaystyle w=m*g} {\displaystyle w=m*g}, or w = m g {\displaystyle w=mg} {\displaystyle w=mg}. Since weight is a force, scientists also write the equation as F = m g {\displaystyle F=mg} {\displaystyle F=mg}. F {\displaystyle F} F = symbol for weight, measured in Newtons, N. m {\displaystyle m} m = symbol for mass, measured in kilograms, or kg. g {\displaystyle g} g = symbol for gravitational acceleration, expressed as m/s, or meters per second squared. If you're using meters, the gravitational acceleration at the Earth's surface is 9.8 m/s. Always use m/s for acceleration, unless you’re instructed to do otherwise. If you're asked to use feet, instead of meters, the gravitational acceleration on Earth is 32.2 ft/s. This is the same unit, it's just converted from meters to feet. Luckily, you’re very unlikely to encounter a problem with acceleration written in ft/s.

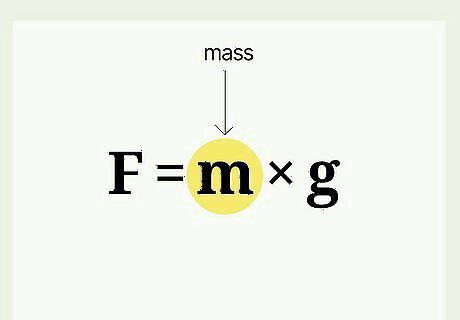
Determine the mass of the object. Because we're trying to get weight from mass, we can assume we already have the mass. Mass is the fundamental amount of matter an object has, and is expressed in kilograms.

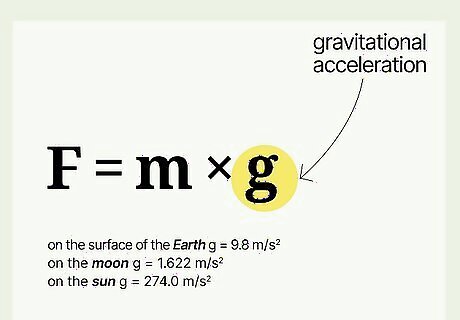
Determine the gravitational acceleration. In other words, figure out what g {\displaystyle g} g is. On the surface of the Earth, g {\displaystyle g} g is 9.8 m/s. Elsewhere in the universe, the acceleration of gravity is different. The gravitational acceleration on the moon is different from the gravitational acceleration on the Earth. Acceleration due to gravity on the moon is about 1.622 m/s, or about 1/6 of the acceleration that it is here on Earth. That's why you weigh 1/6 of your Earth-weight on the moon. The gravitational acceleration on the sun is different from the gravitational acceleration on the Earth and moon. Acceleration due to gravity on the sun is about 274.0 m/s, or about 28 times the acceleration that it is here on Earth. That's why you would weigh 28 times your Earth-weight on the sun (if you could survive!).

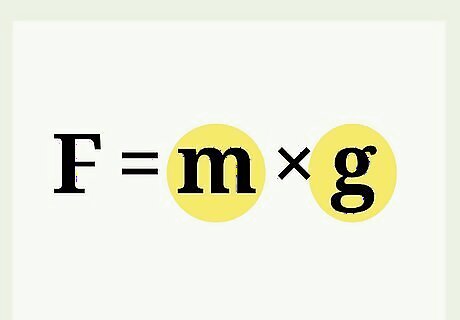
Plug the numbers into the equation F = m g {\displaystyle F=mg} {\displaystyle F=mg}. Now that you've got m {\displaystyle m} m and g {\displaystyle g} g, plug those values into the equation F = m g {\displaystyle F=mg} {\displaystyle F=mg}. You’ll get a number described in Newtons, or N.

Sample Problems

Example #1: An object has a mass of 100 kg. What is its weight on the surface of the Earth? We know m {\displaystyle m} m equals 100 kg, and g {\displaystyle g} g equals 9.8 m/s (since this is the gravitational acceleration on Earth’s surface). Plug these values into the equation: F {\displaystyle F} F = 100 kg * 9.8 m/s. F {\displaystyle F} F = 980 N. In other words, on the surface of the Earth, an object with a mass of 100 kg will weigh about 980 Newtons on Earth.

Example #2: An object has a mass of 40 kg. What is its weight on the surface of the moon? We know m {\displaystyle m} m equals 40 kg, and g {\displaystyle g} g equals 1.6 m/s (since the gravitational acceleration on the Moon’s surface is 1.6 m/s). Plug these values into the equation: F {\displaystyle F} F = 40 kg x 1.6 m/s. F {\displaystyle F} F = 64 N. In other words, on the surface of the moon, an object with a mass of 40 kg will weigh approximately 64 Newtons on the moon.

Example #3: An object weighs 549 Newtons on the surface of the Earth. What is its mass? For this problem, we have to work backward. We have F {\displaystyle F} F and g {\displaystyle g} g, but we need to calculate m {\displaystyle m} m. Set up the equation: 549 = m {\displaystyle m} m * 9.8 m/s. Instead of multiplying m {\displaystyle m} m * g {\displaystyle g} g, we divide F {\displaystyle F} F by g {\displaystyle g} g. In other words, m = F / g {\displaystyle m=F/g} {\displaystyle m=F/g}. Plugging in our values, we get m {\displaystyle m} m = 549/9.8 m/s. m {\displaystyle m} m = 56 kg. In other words, an object weighing 549 Newtons on the surface of the Earth will have a mass of about 56 kilograms.

Catching Mistakes

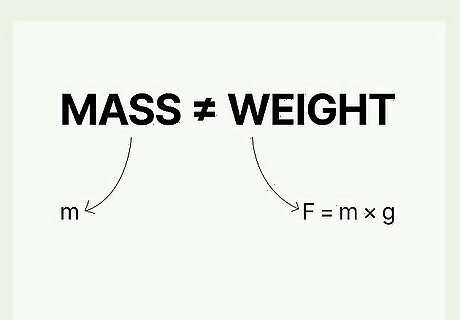
Avoid confusing mass and weight. Remember that mass is the amount of "stuff" in an object, which stays the same no matter where you move it. Weight measures the force of gravity on that "stuff," which changes if you move through space. Try these mnemonic devices to help you memorize your units: Mass is in units of grams or kilograms. Both mass and gram contain an m {\displaystyle m} m. Weight is in units of newtons. Both weight and newton contain a w. You only have weight while you're "wait"ing on Earth, but even "mass"tronauts have mass.

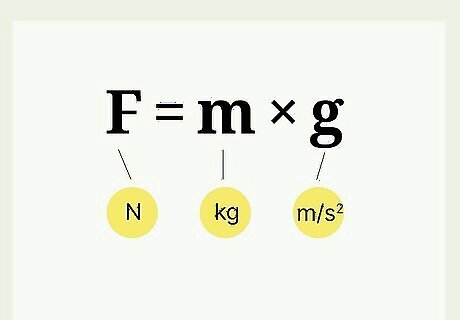
Always use scientific units: kg, N, and m/s. Most physics problems use newtons (N) for weight, meters per second squared (m/s) for gravitational force, and kilograms (kg) for mass. If you use a different unit for one of these values, your calculations will be incorrect. Convert all values to scientific units before plugging them into the standard equation. These conversions may help you out if you're used to the imperial / U.S. system: 1 pound-force = ~4.448 newtons 1 foot = ~0.3048 meters