
views
Asset Price
∗
Discount Rate
1
−
(
1
+
Discount Rate
)
-Periods
+
Annual Maintenance Costs
{\displaystyle {\text{Asset Price}}*{\frac {\text{Discount Rate}}{1-(1+{\text{Discount Rate}})^{\text{-Periods}}}}+{\text{Annual Maintenance Costs}}}
. Let's see how this equation is applied.

Determine the price of the asset. For example, suppose you are comparing two analyzers, A and B, costing $100,000 and $130,000, respectively. These are the Asset Prices.
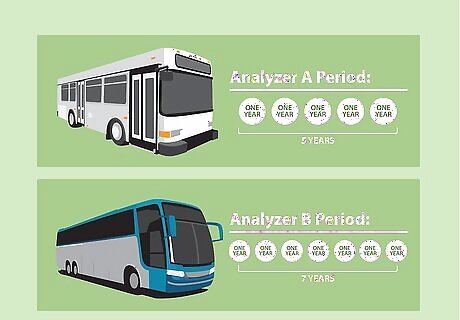
Determine the expected lifespan for each. Suppose Analyzer A is expected to last 5 years, while Analyzer B is expected to last 7 years. These are the number of Periods.
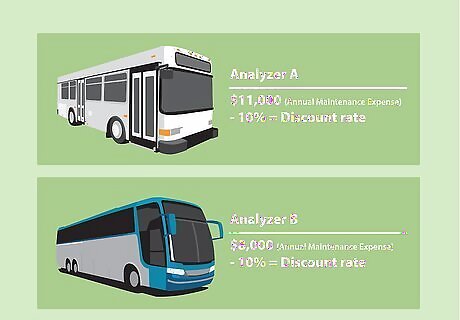
Determine your discount rate. Discount rate is the cost of capital, or how much return your capital is required to generate each year. Say your organization uses a Discount Rate of 10%. Determine the annual maintenance costs for the asset. Suppose Analyzer A has an annual maintenance expense of $11,000, while Analyzer B has annual maintenance expense of $8,000.

Plug the numbers into the equation Asset Price x Discount rate / (1-(1+Discount Rate)^-Periods) + Annual Maintenance Costs. It should be apparent that Analyzer B is the more cost effective option, with a net savings of $2,677.03 a year, compared to Analyzer A. For Analyzer A, EAC = $ 100 , 000 ∗ 0.10 ( 1 − ( 1 + 0.10 ) − 5 ) + $ 11 , 000 = $ 37 , 379.75 {\displaystyle {\text{EAC}}=\$100,000*{\frac {0.10}{(1-(1+0.10)^{-5})}}+\$11,000=\$37,379.75} {\text{EAC}}=\$100,000*{\frac {0.10}{(1-(1+0.10)^{{-5}})}}+\$11,000=\$37,379.75 For Analyzer B, EAC = $ 130 , 000 ∗ 0.10 ( 1 − ( 1 + 0.10 ) − 7 ) + $ 8 , 000 = $ 34 , 702.72 {\displaystyle {\text{EAC}}=\$130,000*{\frac {0.10}{(1-(1+0.10)^{-7})}}+\$8,000=\$34,702.72} {\text{EAC}}=\$130,000*{\frac {0.10}{(1-(1+0.10)^{{-7}})}}+\$8,000=\$34,702.72




















Comments
0 comment