How to Calculate the Growth Rate of Nominal GDP

Calculating Nominal GDP

Understand the distinction between nominal and real GDP. Nominal GDP is the GDP of the country measured at current market prices. Real GDP, on the other hand, is adjusted for inflation or deflation. Many economist use real GDP instead of nominal GDP when determining the growth rate of an economy. Nominal GDP represents the output of the country at current prices, and therefore is useless when comparing output for different periods. For example, knowing that a country's annual nominal GDP was $1 billion in 1940 but $200 billion now does not tell you much about the actual relative output between those two periods. You would have to convert the figures to real GDP to see how they compare.

Add together that period's consumer spending or consumption. Nominal GDP can be calculated by adding together the country's expenditures over the time period. Four categories of spending are added together, the first being consumption. This is the sum that consumers spend on durable goods, non-durable goods, and services. This would include personal items such as food, clothing, rent, and services like health care. Consumption is the largest and most stable part of nominal GDP. However, imported goods are not included, as they are part of the final category, net exports.

Sum all investments. The second part of nominal GDP is investment. This represents all of the money spent on capital equipment, increases in inventory, and structures. Items that would fall into this category include the purchase of business machinery, new homes, and the construction of new factories. Stocks and bonds are not included here since they do not add to any actual output.

Add together all government spending. This is the accumulation of spending by all levels of government on goods and services. Examples include military purchases, teacher pensions and government salaries. Deducted from this amount are government transfer payments such as welfare or unemployment payments.

Determine the net exports. The sum of all imports is calculated and then subtracted from the sum of all exports. The difference between the amount of foreign goods consumed domestically and the amount of domestic goods consumed in foreign countries makes up the net exports. When exports exceed imports, it adds to the amount of GDP. Add up the four categories to arrive at nominal GDP for the time period.

Calculate the GDP for the prior period. In order to calculate your nominal GDP growth rate, you'll need nominal GDP figures for more than one time period. These periods can be consecutive or removed by any number of periods, as long as you have reliable data for each. Check to make sure that your nominal GDPs are for the same time period, for the same nation, and expressed in the same currency.

Calculating Nominal GDP Growth Rate

Set up your equation. The simplest way to calculate nominal GDP growth is by analyzing two consecutive periods. For this type of calculation, the formula is simply the one for percent change. Specifically, it is NGDP Growth = N G D P x − N G D P x − 1 N G D P x − 1 {\displaystyle {\text{NGDP Growth}}={\frac {NGDP_{x}-NGDP_{x-1}}{NGDP_{x-1}}}} {\text{NGDP Growth}}={\frac {NGDP_{{x}}-NGDP_{{x-1}}}{NGDP_{{x-1}}}}. In the formula, N G D P x {\displaystyle NGDP_{x}} NGDP_{{x}} represents the later period and N G D P x − 1 {\displaystyle NGDP_{x-1}} NGDP_{{x-1}} is the earlier. Enter your own data to calculate nominal GDP growth. For example, if NGDP were $200 billion one period and $210 the next, your equation would be: NGDP Growth = $ 210 B − $ 200 B $ 200 B {\displaystyle {\text{NGDP Growth}}={\frac {\$210B-\$200B}{\$200B}}} {\text{NGDP Growth}}={\frac {\$210B-\$200B}{\$200B}}

Calculate simple GDP growth. Simply perform the subtraction and division specified by the equation to solve. Your answer will be a decimal and must be multiplied by 100 to arrive at your growth rate in percentage form. Using the previous example, the equation would first solve to NGDP Growth = $ 10 B $ 200 B {\displaystyle {\text{NGDP Growth}}={\frac {\$10B}{\$200B}}} {\text{NGDP Growth}}={\frac {\$10B}{\$200B}}. Then, dividing gives NGDP Growth = 0.05 {\displaystyle {\text{NGDP Growth}}=0.05} {\text{NGDP Growth}}=0.05. Finally, multiply by 100 to get NGDP Growth = 5 % {\displaystyle {\text{NGDP Growth}}=5\%} {\text{NGDP Growth}}=5\%. Your nominal GDP growth rate between the two periods is 5 percent.

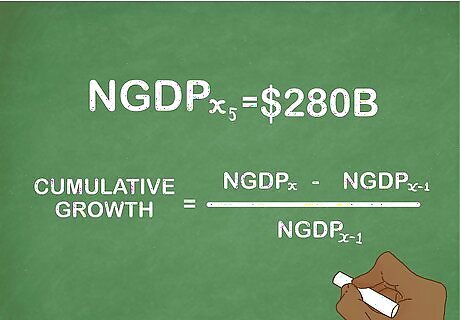
Find cumulative growth over a longer time period. Cumulative growth refers to the total growth in nominal GDP between non-consecutive periods. It is calculated the same way as consecutive growth, by substituting N G D P x {\displaystyle NGDP_{x}} NGDP_{{x}} for a later period and N G D P x − 1 {\displaystyle NGDP_{x-1}} NGDP_{{x-1}} for the earlier one. Use the method described for calculating simple NGDP growth to find cumulative growth. For example, imagine that a record of nominal GDP growth shows a value of $200 billion one year and $280 billion five years later. The cumulative growth can be calculated as 40 percent using the above method.

Convert cumulative growth to average growth. Average growth can show you how much a figure grew each period during a longer time period. You might think that the average growth would simply be the cumulative growth divided by the number of periods, but this is not the case. Average growth is calculated using a different formula. The formula, specific to calculating NGDP, can be expressed as NGDP Growth = ( N G D P x N G D P x − 1 ) 1 t − 1 {\displaystyle {\text{NGDP Growth}}=({\frac {NGDP_{x}}{NGDP_{x-1}}})^{\frac {1}{t}}-1} {\text{NGDP Growth}}=({\frac {NGDP_{{x}}}{NGDP_{{x-1}}}})^{{{\frac {1}{t}}}}-1. The variable t {\displaystyle t} t represents the number of time periods. So, continuing with the cumulative growth example, we would have NGDP Growth = ( $ 280 B $ 200 ) 1 5 − 1 {\displaystyle {\text{NGDP Growth}}=({\frac {\$280B}{\$200}})^{\frac {1}{5}}-1} {\text{NGDP Growth}}=({\frac {\$280B}{\$200}})^{{{\frac {1}{5}}}}-1. This would then simplify to NGDP Growth = ( 1.4 ) 1 5 − 1 {\displaystyle {\text{NGDP Growth}}=(1.4)^{\frac {1}{5}}-1} {\text{NGDP Growth}}=(1.4)^{{{\frac {1}{5}}}}-1. Then, the exponent can be solved by raising 1.4 to the power of 1 divided by 5, or 0.2. This is done on a calculator using the exponent button or can be entered into a search engine as "1.4^0.2". The result is 1.0696 when rounded to four decimal places. This leaves the equation as NGDP Growth = 1.0696 − 1 {\displaystyle {\text{NGDP Growth}}=1.0696-1} {\text{NGDP Growth}}=1.0696-1. So, the result is NGDP Growth = 0.0696 {\displaystyle {\text{NGDP Growth}}=0.0696} {\text{NGDP Growth}}=0.0696. Multiplying by 100, we get the average growth rate over the time period, which is 6.96 percent.

Using Nominal GDP Growth

Figure out the total output of a nation. The primary function of nominal GDP is to express the total output of a country over a time period (usually a quarter or year) at its present market value. Nominal GDP growth can then be used to find the growth or decrease in output between years with inflation or deflation included. While this growth may not serve as a reliable measure of actual output between years, comparing market values between years can be useful for other purposes.

Assess inflation. The primary use of nominal GDP growth is to measure inflation between years. Real GDP growth is calculated for the same set of years. Then, the two growth rates are compared to assess inflation. If nominal GDP is rising faster than real GDP, the country's currency is experiencing inflation. If nominal GDP is growing at a slower rate, the country is experiencing deflation.

Convert to real GDP. Real GDP adds one more step to the summation of nominal GDP by factoring out inflation or deflation from GDP. The nominal GDP is modified by the GDP deflator, a measure of relative prices, to arrive at real GDP. The GDP deflator is composed of price indexes for the two periods being compared. For example, the price indexes of two years might be 105 for a base year and 120 for the current. The GDP deflator to convert nominal GDP for the current year to real GDP would then be 105 ÷ 120 {\displaystyle 105\div 120} 105\div 120, or 0.875. So, if the nominal GDP for that year were $100 billion, real GDP would be 0.875 × $ 100 b i l l i o n {\displaystyle 0.875\times \$100billion} 0.875\times \$100billion, or $87.5 billion.