views
Check to see that your data meets the following criteria: Data should usually be normally distributed revolving around a mean (average). In the example below, a bottle company fills their bottles to 16 oz. (mean); they are evaluating if their process is “in-control”. The amount in ounces over 16 oz. is normally distributed around the mean. Measurements need to be independent of one another. In the example, the measurements are in subgroups. The data in the subgroups should be independent of the measurement number; each data point will have a subgroup and a measurement number.
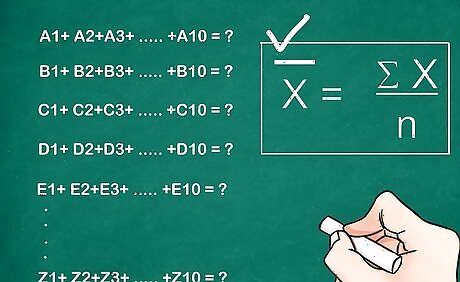
Find the mean of each subgroup. To find the mean, add all measurements in the subgroup and divide by the number of measurements in the subgroup. In the example, there are 20 subgroups and in each subgroup there are 4 measurements.
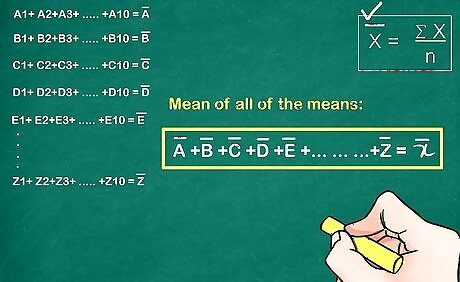
Find the mean of all of the means from the previous step (X). This will give you the overall mean of all the data points. The overall mean will be the centerline in the graph (CL), which is 13.75 for our example.

Calculate the standard deviation (S) of the data points (see tips).

Calculate the upper and lower control limits (UCL, LCL) using the following formula: UCL = CL + 3*S LCL = CL – 3*S The formula represents 3 standard deviations above and 3 standard deviations below the mean respectively.
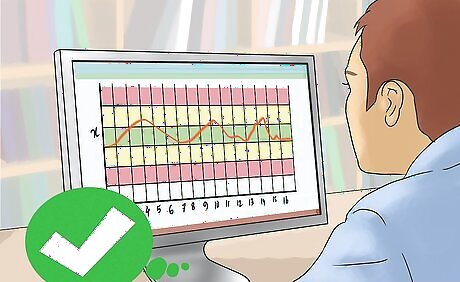
Refer to the below chart with steps 7 through 10.
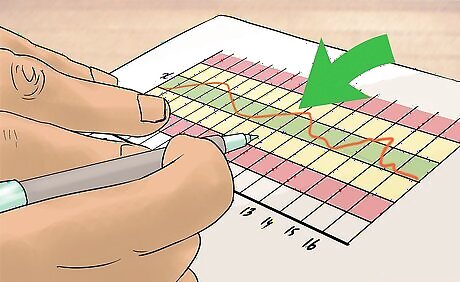
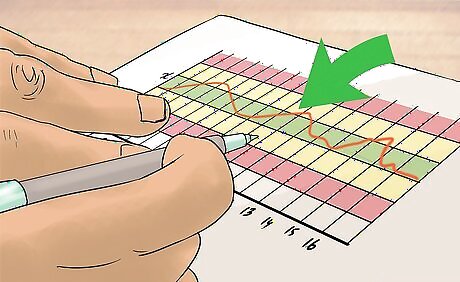
Draw a line at each deviation. In the above example, there is a line drawn at one, two, and three standard deviations (sigma's) away from the mean. Zone C is 1 sigma away from the mean (green). Zone B is 2 sigma away from the mean (yellow). Zone A is 3 sigma away from the mean (red).
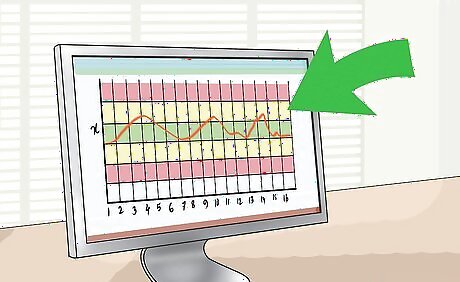
Graph the X-bar Control Chart, by graphing the subgroup means (x-axis) verses measurements (y-axis). Your graph should look like something like this:
Evaluate the graph to see if the process is out-of-control. The graph is out-of-control if any of the following are true: Any point falls beyond the red zone (above or below the 3-sigma line). 8 consecutive points fall on one side of the centerline. 2 of 3 consecutive points fall within zone A. 4 of 5 consecutive points fall within zone A and/or zone B. 15 consecutive points are within Zone C. 8 consecutive points not in zone C.

State whether the system is in-control or out-of-control.



















Comments
0 comment