How to Do Well in Calculus

Building a Strong Foundation

Schedule yourself for building block classes. If you know, as a young student, that you will want to take calculus, either in high school or later in college, you should start with your class schedule. Tell your guidance counselor that you want to get into calculus and map out a schedule that will do this for you. You will need to take at least the basic preliminary classes of Algebra (sometimes taught in one or two years), Geometry, and Trigonometry (sometimes labeled as “Pre-Calculus”). If your school offers different academic levels of math classes, such as basic, standard, honors, or so on, you should try to get into the highest level that you can.

Master the basics of algebra. Many students begin learning the basics of algebra in seventh or eighth grade. Some even begin getting some basic principles earlier than that. You need to work hard in these classes. Math is a subject that builds one class on another. If you have trouble with the basics that begin in algebra, you are likely to have even more difficulty later in calculus. In particular, here are some of the skills that you should develop: Manipulation of equations Quadratic equations Powers and roots

Study particularly hard in trigonometry. In most math programs, the subject that comes just before calculus is trigonometry. Trigonometry is based on the ratios of the sides of right triangles, particularly in connection with the unit circle. Trigonometric functions relate very well to describing motion, and calculus is based on measuring rates of change. Therefore, trigonometry is a key building block of calculus. In particular, you need to learn the following topics very thoroughly: Basic trigonometry functions: sine, cosine, tangent, secant, cosecant, cotangent Inverse trigonometry functions: arcsine, arccosine, arctangent Know substitute functions. A lot of trigonometry is based on substituting one function for another. You will need to be able to use these substitutions quickly and easily to do well in calculus. Double angles like sin ⁡ 2 θ {\displaystyle \sin 2\theta } \sin 2\theta Half angles, like sin 2 ⁡ θ 2 {\displaystyle \sin ^{2}{\frac {\theta }{2}}} \sin ^{{2}}{\frac {\theta }{2}} Addition formulas, such as cos ⁡ ( x + y ) {\displaystyle \cos(x+y)} \cos(x+y)

Gain comfort with exponents and logarithms. Exponents and logarithms are key to manipulating equations and functions in calculus. These topics generally arise initially in algebra and pre-calculus classes. Exponents and logarithms are inverse operations of each other, and are key to many operations in calculus. You need to study these carefully. Go back and review these topics before your calculus class, if necessary.

Mastering the Basics of Calculus

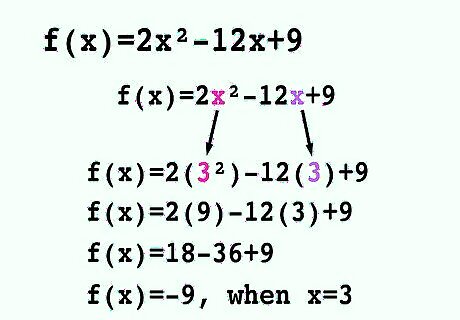
Understand the concept of functions. Most calculus text books begin with a review of functions. A function is generally described as a mapping from one set of numbers, called the domain of the function, to another set, called the range. In simple form, if you put one number in to the function, you get another number out. Some simple functions are: Constant functions. An example is f ( x ) = 3 {\displaystyle f(x)=3} f(x)=3. Linear functions. These are functions whose graphs form straight lines. An example is f ( x ) = 2 x − 7 {\displaystyle f(x)=2x-7} f(x)=2x-7. Quadratic functions. A simple quadratic function forms a parabola, such as f ( x ) = x 2 + 3 x − 2 {\displaystyle f(x)=x^{2}+3x-2} f(x)=x^{2}+3x-2. Power functions. These are variations or advancements on the quadratic function, including such functions as f ( x ) = x 1 2 {\displaystyle f(x)=x^{\frac {1}{2}}} f(x)=x^{{{\frac {1}{2}}}} or f ( x ) = x − 1 = 1 x {\displaystyle f(x)=x^{-1}={\frac {1}{x}}} f(x)=x^{{-1}}={\frac {1}{x}}.

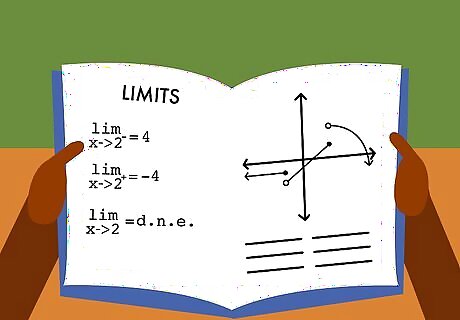
Review the concept of limits. Calculus rests primarily on the concept of mathematical limits. This is the theoretical idea of numbers getting infinitely small or infinitely large, and then measuring the results. Using limits leads to many of the derivations and other concepts that you study in calculus.

Memorize certain rules of manipulating derivatives. As you begin studying the concept of derivatives in calculus, you will learn certain rules that help in manipulating functions and resolving problems. You will need to memorize these rules so they come to you quickly when you need them. These basic rules are: Product rule. The derivative of f ( x ) g ( x ) = f ′ ( x ) g ( x ) + f ( x ) g ′ ( x ) {\displaystyle f(x)g(x)=f^{\prime }(x)g(x)+f(x)g^{\prime }(x)} f(x)g(x)=f^{{\prime }}(x)g(x)+f(x)g^{{\prime }}(x). Chain rule. The derivative of f ( g ( x ) ) = f ′ ( g ) ∗ g ′ ( x ) {\displaystyle f(g(x))=f^{\prime }(g)*g^{\prime }(x)} f(g(x))=f^{{\prime }}(g)*g^{{\prime }}(x). Quotient rule. If f {\displaystyle f} f and g {\displaystyle g} g are both functions, then: ( f g ) ′ = f ′ g − g ′ f g 2 {\displaystyle ({\frac {f}{g}})^{\prime }={\frac {f^{\prime }g-g^{\prime }f}{g^{2}}}} ({\frac {f}{g}})^{{\prime }}={\frac {f^{{\prime }}g-g^{{\prime }}f}{g^{2}}}

Memorize derivatives of basic trig functions. As with many of the rules of trigonometry, you want the derivatives to be tools that you can use and not additional problems to solve every time they arise. You will be using trigonometric functions over and over, so you should memorize the basic derivatives of them: ( sin ⁡ x ) ′ = cos ⁡ x {\displaystyle (\sin x)^{\prime }=\cos x} (\sin x)^{{\prime }}=\cos x ( cos ⁡ x ) ′ = − sin ⁡ x {\displaystyle (\cos x)^{\prime }=-\sin x} (\cos x)^{{\prime }}=-\sin x ( tan ⁡ x ) ′ = sec 2 ⁡ x {\displaystyle (\tan x)^{\prime }=\sec ^{2}x} (\tan x)^{{\prime }}=\sec ^{{2}}x ( cot ⁡ x ) ′ = − csc 2 ⁡ x {\displaystyle (\cot x)^{\prime }=-\csc ^{2}x} (\cot x)^{{\prime }}=-\csc ^{{2}}x ( sec ⁡ x ) ′ = sec ⁡ x tan ⁡ x {\displaystyle (\sec x)^{\prime }=\sec x\tan x} (\sec x)^{{\prime }}=\sec x\tan x ( csc ⁡ x ) ′ = − csc ⁡ x cot ⁡ x {\displaystyle (\csc x)^{\prime }=-\csc x\cot x} (\csc x)^{{\prime }}=-\csc x\cot x

Being a Strong Calculus Student

Prepare for class. Calculus is a subject that moves very quickly. You cannot always expect the teacher or professor to slow the presentation for you to keep up. You should review the course outline, know the topic of each class lecture, and do the reading from your text in advance. As you read, highlight or underline key topics. Make note of particular concepts that you do not understand. Prepare questions for class. Realize as you read that the lecture may help explain things to you. Even so, prepare some questions in case you remain confused.

Attend all classes and tutorial sessions. Calculus is a complicated subject, and you cannot expect to learn it completely on your own. In lectures, the teacher may give you added tips or hints for solving particular problem types. You may also get insights into what the teacher believes is most important for testing.

Do all homework problems. The best way to learn any subject - particularly in math - is to use it repeatedly for solving problems. Between classes, you should complete all assigned homework. If you really want to do well, seek out additional work. For example, some teachers may make a practice of assigning only the even numbered homework problems. If you really want to learn the material well, go beyond the assignment and do all the problems. Check your work carefully and look for errors before turning in your homework.

Work with a study group. Advanced subjects like calculus lend themselves well to study groups. Find some other students in your class and suggest working together. Working in a group, you can help each other understand difficult concepts. You can also check each other’s homework and review ideas. Make sure that your study group is productive and spends the time working. Hold each member of the group responsible for doing his or her own work. If someone is not meeting expectations, you may want to ask that person to leave the group. Productive group sizes are about four to six students.

Know the content of each exam. Before you go into any exam, make sure you know what it will cover. Usually this is just a matter of reviewing your course syllabus. However, if you have any questions, you should check with your professor or teaching assistant. Carefully study all the issues that will be covered on the exam.