How to Find the Effective Interest Rate

• The effective interest rate is higher than the nominal interest rate because it takes compounding interest into account.
• Use the formula ${\displaystyle r=(1+i/n)^{n}-1}$ to calculate the effective interest rate.
• For interest that compounds continuously, use the formula ${\displaystyle r=e^{i}-1}$ to calculate the effective interest rate.

Understanding Effective Interest Rate

Familiarize yourself with the concept of an effective interest rate. The effective interest rate describes the full cost of borrowing. It takes into account the effect of compounding interest, which is left out of the nominal or "stated" interest rate. For example, a loan with 10% interest compounded monthly will carry an interest rate higher than just 10%. This is because more interest is accumulated each month. The effective interest rate calculation does not take into account one-time fees like loan origination fees. These fees are considered, however, in the calculation of the annual percentage rate.

Determine the stated interest rate. The stated (also called nominal) interest rate is the interest rate that is typically quoted to you. Think of it as the "headline" interest rate that lenders usually advertise on loans, investments, and savings accounts. The stated interest rate is expressed as a percentage. For example, if you’re shopping for a savings account, Bank A might advertise an interest rate of 2% while Bank B has an interest rate of 3%. These are their stated or nominal interest rates.

Check the number of compounding periods for the loan. The compounding periods are generally monthly, quarterly, annually, or continuously. This refers to how often the interest is applied. Usually, the compounding period is monthly. You'll still want to check with your lender to verify that, though.

Calculating the Effective Interest Rate

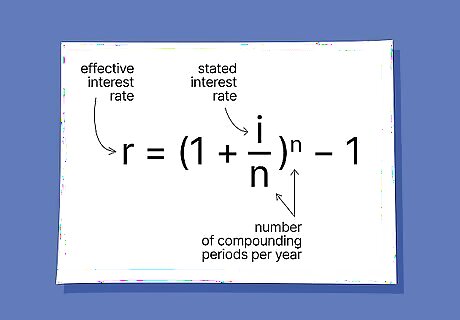
Learn the formula to convert a stated interest rate to an effective interest rate. The effective interest rate is calculated using a simple formula: r = ( 1 + i / n ) n − 1. {\displaystyle r=(1+i/n)^{n}-1.} {\displaystyle r=(1+i/n)^{n}-1.} In this formula, r represents the effective interest rate, i represents the stated interest rate, and n represents the number of compounding periods per year.

Calculate the effective interest rate using the formula above. For example, consider a loan with a stated interest rate of 5% that is compounded monthly. Plug this information into the formula to get: r = (1 + .05/12) - 1, or r = 5.12%. The same loan compounded daily yields: r = (1 + .05/365) - 1, or r = 5.13%. Note that the effective interest rate is always greater than the stated rate.

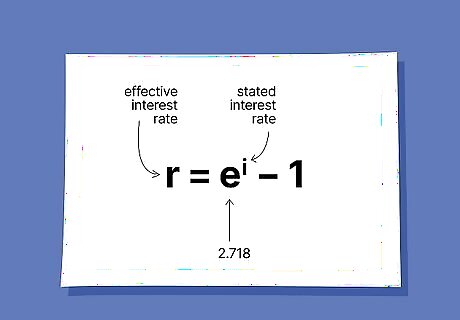
Use a different formula if interest is continuously compounded. If interest is compounded continuously, you calculate the effective interest rate using a different formula: r = e i − 1 {\displaystyle r=e^{i}-1} {\displaystyle r=e^{i}-1}. In this formula, r is the effective interest rate, i is the stated interest rate, and e is the constant 2.718.

Calculate the effective interest rate for continuously compounding interest. For example, consider a loan with a nominal interest rate of 9% compounded continuously. The formula above yields: r = 2.718 - 1, or 9.417%.

Use a simplified method to calculate the effective interest rate. After reading and fully understanding the theory behind effective interest rates, there is a simpler way to find it: Use the formula ((Number of intervals × 100 + interest) ÷ (Number of intervals × 100)) × 100 Find the number of intervals per year. A semi-annual rate is compounded 2 times each year, quarterly is 4, monthly is 12, and daily is 365. Multiply the number of intervals per year by 100 then add the interest rate. If the interest rate is 5%, for semi-annual compounding it is (2 × 100 + 5%) or 205. For quarterly it is 405, 1,205 for monthly, and 36,505 for daily compounding. Plug your information into the above formula to find the effective interest rate: Semi-annually: ((Number of intervals × 100 + interest) ÷ (Number of intervals × 100)) × 100 = ((205)÷(200)) × 100 = 105.0625 Quarterly: ((405)÷(400)) ×100 = 105.095 Monthly: ((1,205)÷(1,200)) ×100=105.116 Daily: ((36,505)÷(36,500)) ×100 = 105.127 The effective interest is the value exceeding 100 when the principal is 100. The value exceeding 100 for the semi-annual calculation is 5.0625%. So, that is the effective interest rate for semi-annual. For quarterly compounding it is 5.095%, 5.116% for monthly, and 5.127% for daily.