views
Graphing a Linear Inequality on a Number Line
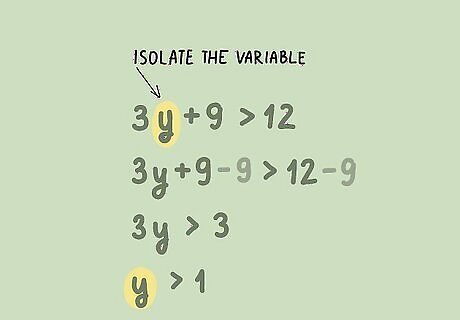
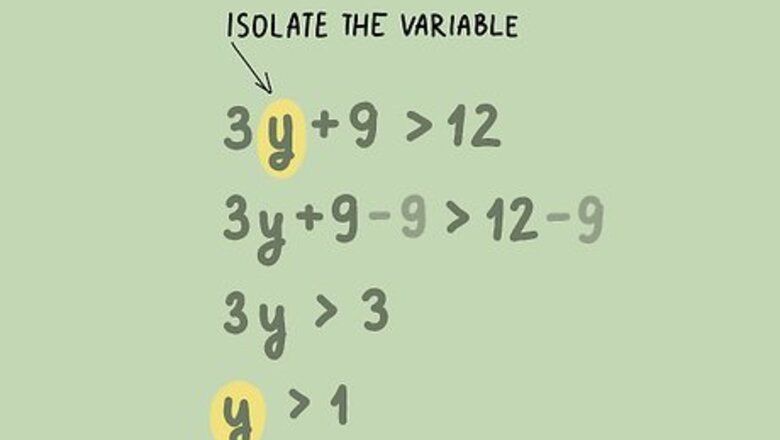
Solve for the variable. To solve the inequality isolate the variable using the same algebraic methods you would use to solve an equation. Remember that when you multiply or divide by a negative number, you need to flip the inequality sign. For example, if you are solving the inequality 3 y + 9 > 12 {\displaystyle 3y+9>12} 3y+9>12, isolate the variable by subtracting 9 from each side of the inequality, then dividing by 3: 3 y + 9 > 12 {\displaystyle 3y+9>12} 3y+9>12 3 y + 9 − 9 > 12 − 9 {\displaystyle 3y+9-9>12-9} 3y+9-9>12-9 3 y > 3 {\displaystyle 3y>3} 3y>3 3 y 3 > 3 3 {\displaystyle {\frac {3y}{3}}>{\frac {3}{3}}} {\frac {3y}{3}}>{\frac {3}{3}} y > 1 {\displaystyle y>1} y>1 Your inequality should only have one variable. If your inequality has two variables, it is more appropriate to graph it on a coordinate plane using another method.
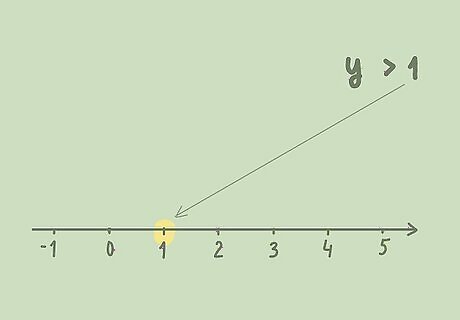
Draw a number line. Include the relative value on your number line (the value you found the variable to be less than, greater than, or equal to). Make the number line as long or short as required. For example, if you found that y > 1 {\displaystyle y>1} y>1, make sure to include a point for 1 on the number line.
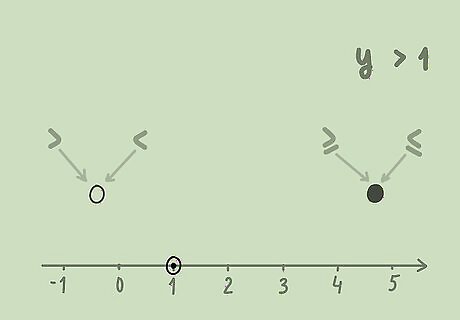
Draw a circle indicating the relative value. If the value is less than ( < {\displaystyle <} ) or greater than ( > {\displaystyle >} >) this number, the circle should be open, since the solution does not include the value. If the value is less than or equal to ( ≤ {\displaystyle \leq } \leq ), or greater than or equal to ( ≥ {\displaystyle \geq } \geq ), the circle should be filled in, since the solution includes the value. For example, if y > 1 {\displaystyle y>1} y>1, you would draw a circle at 1 on the number line. You would not fill in the circle, since 1 is not included in the solution.
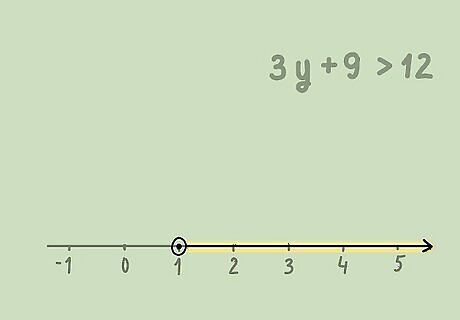
Draw an arrow indicating the included values. If the variable is greater than the relative value, your arrow should point to the right, since the solution includes values greater than that number. If the variable is less than the relative value, your arrow should point to the left, since the solution includes values less than that number. For example, for the solution y > 1 {\displaystyle y>1} y>1, you would draw an arrow pointing to the right, since the solution includes values greater than 1.
Graphing a Linear Inequality on a Coordinate Plane
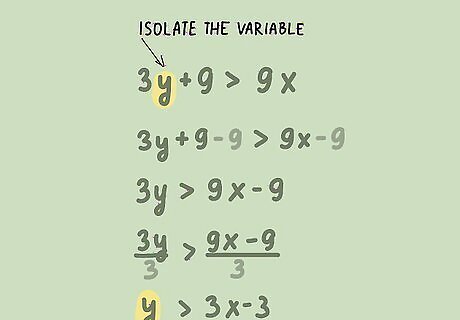
Solve for y {\displaystyle y} y. You want to find the equation of the line, so to do this you need to isolate the y {\displaystyle y} y variable on the left side of the equation using algebra. The right side of the equation should have the x {\displaystyle x} x variable, and likely, a constant. For example, for the inequality 3 y + 9 > 9 x {\displaystyle 3y+9>9x} 3y+9>9x, you would isolate the y variable by subtracting 9 from both sides, then dividing by 3: 3 y + 9 > 9 x {\displaystyle 3y+9>9x} 3y+9>9x 3 y + 9 − 9 > 9 x − 9 {\displaystyle 3y+9-9>9x-9} 3y+9-9>9x-9 3 y > 9 x − 9 {\displaystyle 3y>9x-9} 3y>9x-9 3 y 3 > 9 x − 9 3 {\displaystyle {\frac {3y}{3}}>{\frac {9x-9}{3}}} {\frac {3y}{3}}>{\frac {9x-9}{3}} y > 3 x − 3 {\displaystyle y>3x-3} y>3x-3
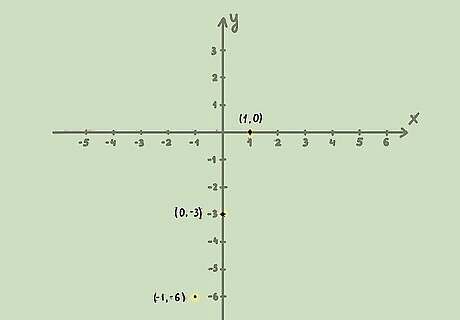
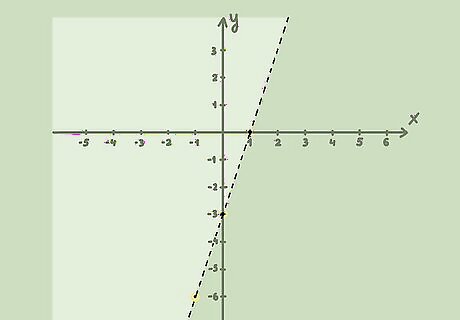
Graph the line on a coordinate plane. To do this, turn the inequality into an equation, and graph as you would any equation of a line. Plot the y-intercept, then use the slope to graph other points on the line. For example, if the inequality is y > 3 x − 3 {\displaystyle y>3x-3} y>3x-3, you would graph the line y = 3 x − 3 {\displaystyle y=3x-3} y=3x-3. The y-intercept (the point where the line crosses the y axis) is -3, and the slope is 3, or 3 1 {\displaystyle {\frac {3}{1}}} {\frac {3}{1}}. So, you would draw a point at ( 0 , − 3 ) {\displaystyle (0,-3)} (0,-3). The point above the y-intercept is ( 1 , 0 ) {\displaystyle (1,0)} (1,0). The point below the y-intercept is ( − 1 , − 6 ) {\displaystyle (-1,-6)} (-1,-6).
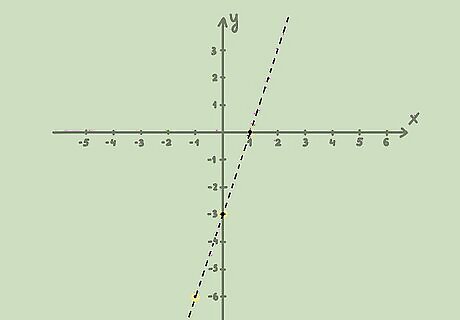
Draw the line. If the inequality is less than ( < {\displaystyle <} ) or greater than ( > {\displaystyle >} >), the line should be dashed, since the solution does not include values equal to the line. If the value is less than or equal to ( ≤ {\displaystyle \leq } \leq ), or greater than or equal to ( ≥ {\displaystyle \geq } \geq ), the line should be solid, since the solution includes values equal to the line. For example, since the inequality is y > 3 x − 3 {\displaystyle y>3x-3} y>3x-3, the line should be dashed, since the values do not include points on the line.
Shade in the appropriate area. If the inequality shows
y
>
m
x
+
b
{\displaystyle y>mx+b}
y>mx+b you should shade in the area above the line. If the inequality shows
y
<
m
x
+
b
{\displaystyle y
Graphing a Quadratic Inequality on a Coordinate Plane
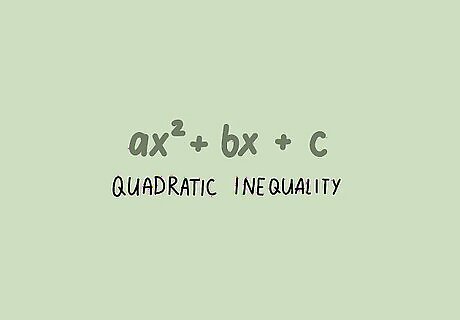
Determine whether you have a quadratic inequality. A quadratic inequality takes the form of
a
x
2
+
b
x
+
c
{\displaystyle ax^{2}+bx+c}
ax^{{2}}+bx+c. Sometimes there may not be an
x
{\displaystyle x}
x term or a constant, but there should always be an
x
2
{\displaystyle x^{2}}
x^{{2}} term on one side of the inequality, and an isolated
y
{\displaystyle y}
y variable on the other side.
For example, you might need to graph the inequality
y
<
x
2
−
10
x
+
16
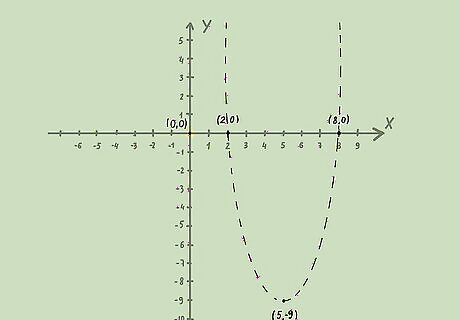
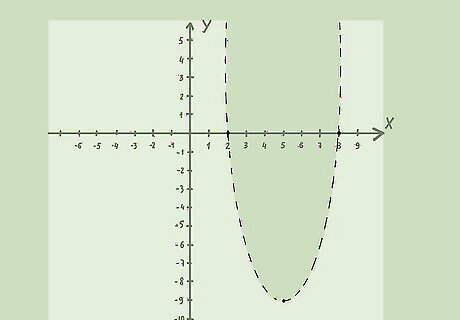
{\displaystyle y Graph the line on a coordinate plane. To do this, turn the inequality into an equation, and graph the line as you normally would. Since you have a quadratic equation, the line will be a parabola.
For example, for the inequality
y
<
x
2
−
10
x
+
16
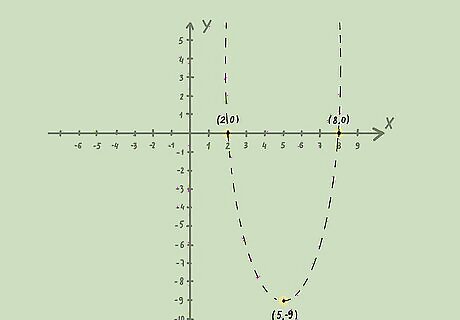
{\displaystyle y Draw the parabola. Draw the parabola with a dashed line if the inequality is less than (
<
{\displaystyle <}
) or greater than (
>
{\displaystyle >}
>). If the value is less than or equal to (
≤
{\displaystyle \leq }
\leq ), or greater than or equal to (
≥
{\displaystyle \geq }
\geq ), you should draw the parabola with a solid line, since the solution includes values equal to the line.
For example, for the inequality
y
<
x
2
−
10
x
+
16
{\displaystyle y Find some test points. In order to determine which area to shade, you need to pick points from inside the parabola, and from outside the parabola.
For example, the graph of the inequality
y
<
x
2
−
10
x
+
16
{\displaystyle y Shade the appropriate area. To determine which area to shade, plug the values of
x
{\displaystyle x}
x and
y
{\displaystyle y}
y from your test points into the original inequality. Whichever point produces a true inequality indicates which area of the graph should be shaded in.
For example, plugging the values of
x
{\displaystyle x}
x and
y
{\displaystyle y}
y of the point
(
0
,
0
)
{\displaystyle (0,0)}
(0,0) into the original inequality, you get:
y
<
x
2
−
10
x
+
16
{\displaystyle y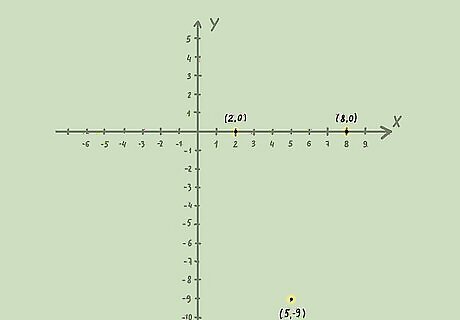



















Comments
0 comment