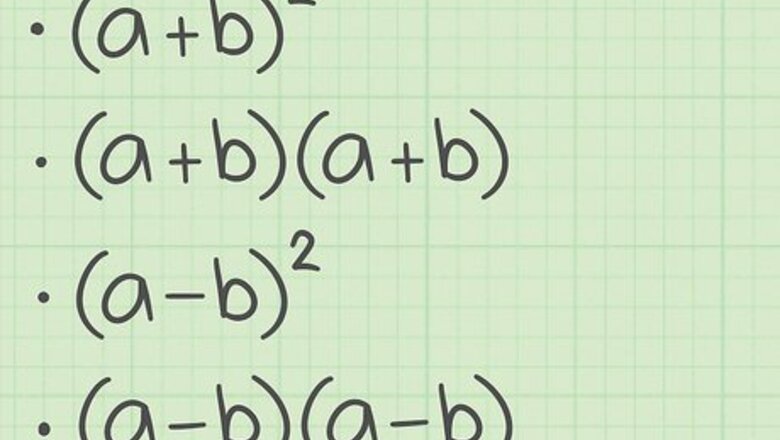
views
(
a
+
b
)
2
=
a
2
+
2
a
b
+
b
2
{\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}
. You can also use this formula to determine whether a trinomial is a perfect square, and to quickly factor those trinomials.
Expanding a Perfect Square
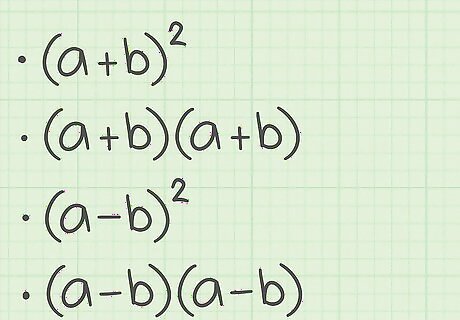
Determine whether you have a perfect square binomial. A binomial is a two-termed expression. If the binomial expression is a perfect square, it will be expressed as either ( a + b ) 2 {\displaystyle (a+b)^{2}} (a+b)^{{2}} or ( a + b ) ( a + b ) {\displaystyle (a+b)(a+b)} (a+b)(a+b). Note the binomials could also have a subtraction symbol. For example, ( 5 y + 3 ) 2 {\displaystyle (5y+3)^{2}} (5y+3)^{{2}} is a perfect square binomial.
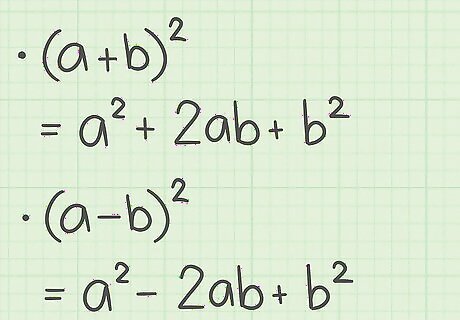
Set up the formula for a perfect square trinomial. The formula is ( a + b ) 2 = a 2 + 2 a b + b 2 {\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}} (a+b)^{{2}}=a^{{2}}+2ab+b^{{2}}. If the binomials show subtraction, the formula is ( a − b ) 2 = a 2 − 2 a b + b 2 {\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}} (a-b)^{{2}}=a^{{2}}-2ab+b^{{2}}. Note that a {\displaystyle a} a is the first term of the binomial, and b {\displaystyle b} b is the second term of the binomial.
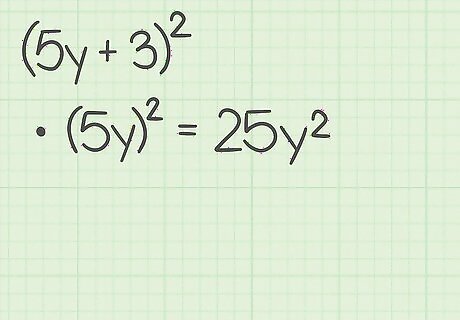
Square the first term of the binomial. This will become the first term of the trinomial. Remember that squaring a term means to multiply it by itself. For example, if you are expanding ( 5 y + 3 ) 2 {\displaystyle (5y+3)^{2}} (5y+3)^{{2}}, you would first calculate ( 5 y ) 2 = 25 y 2 {\displaystyle (5y)^{2}=25y^{2}} (5y)^{{2}}=25y^{{2}}. So, 25 y 2 {\displaystyle 25y^{2}} 25y^{{2}} is the first term of the trinomial.
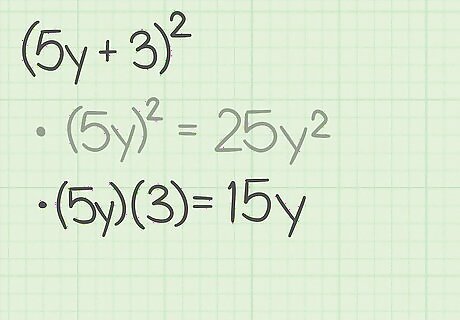
Multiply the first and last term. Make sure you are using the original a {\displaystyle a} a and b {\displaystyle b} b terms from the binomial expression. For example, if you are expanding ( 5 y + 3 ) 2 {\displaystyle (5y+3)^{2}} (5y+3)^{{2}}, you would calculate ( 5 y ) ( 3 ) = 15 y {\displaystyle (5y)(3)=15y} (5y)(3)=15y.
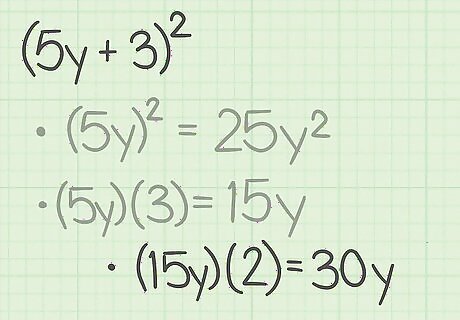
Multiply the product by 2. If the binomials show subtraction, you should multiply by -2. The result will be the middle term in the trinomial. For example, ( 2 ) ( 15 y ) = 30 y {\displaystyle (2)(15y)=30y} (2)(15y)=30y. So, your trinomial now looks like this: 25 y 2 + 30 y + b 2 {\displaystyle 25y^{2}+30y+b^{2}} 25y^{{2}}+30y+b^{{2}}.
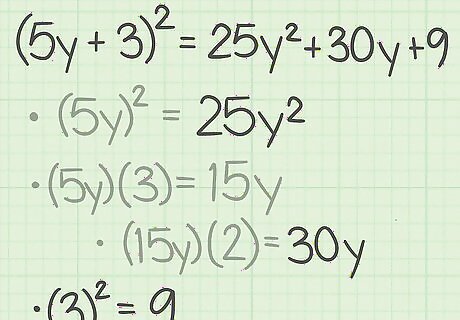
Square the last term. Again, make sure you are using the original b {\displaystyle b} b term from the binomial expression. The square will give you the last term in the trinomial. For example, 3 2 = 9 {\displaystyle 3^{2}=9} 3^{{2}}=9. So, ( 5 y + 3 ) 2 = 25 y 2 + 30 y + 9 {\displaystyle (5y+3)^{2}=25y^{2}+30y+9} (5y+3)^{{2}}=25y^{{2}}+30y+9
Identifying a Perfect Square Trinomial
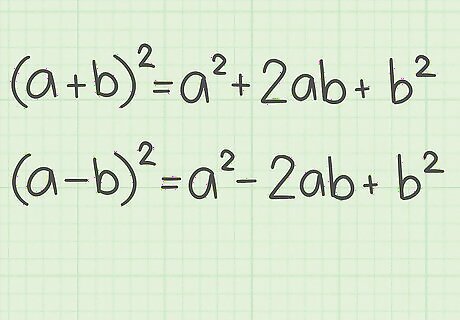
Recall the formula for a perfect square trinomial. The formula is ( a + b ) 2 = a 2 + 2 a b + b 2 {\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}} (a+b)^{{2}}=a^{{2}}+2ab+b^{{2}}. If the binomials show subtraction, the formula is ( a − b ) 2 = a 2 − 2 a b + b 2 {\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}} (a-b)^{{2}}=a^{{2}}-2ab+b^{{2}}
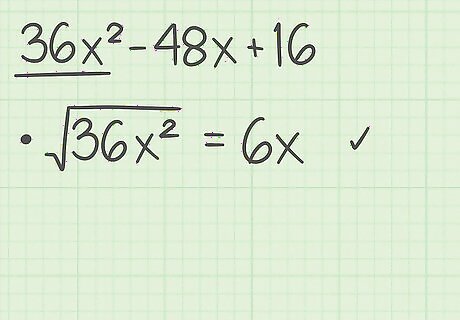
Determine whether the first term in the trinomial is a perfect square. A perfect square is a number whose square root is a whole number. Since the first term in the perfect square formula is a 2 {\displaystyle a^{2}} a^{{2}}, the first term in your trinomial must be a perfect square. Note that the square root of the first term is equal to a {\displaystyle a} a in the squared binomial. For example, in the trinomial 36 x 2 − 48 x + 16 {\displaystyle 36x^{2}-48x+16} 36x^{{2}}-48x+16, the first term is 36 x 2 {\displaystyle 36x^{2}} 36x^{{2}}. The square root of 36 x 2 {\displaystyle 36x^{2}} 36x^{{2}} is 6 x {\displaystyle 6x} 6x. So, the first term of this trinomial is a perfect square. Also, in the squared binomial, a = 6 x {\displaystyle a=6x} a=6x.
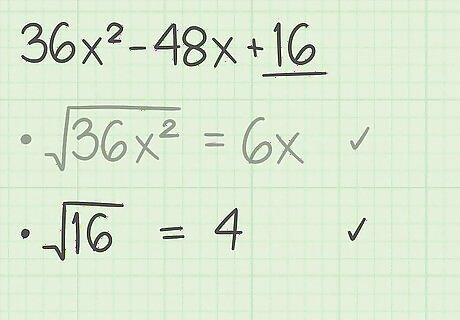
Determine whether the last term of the trinomial is a perfect square. Since the last term in the perfect square formula is b 2 {\displaystyle b^{2}} b^{{2}}, the last term in your trinomial must be a perfect square. Note that the square root of the last term is equal to b {\displaystyle b} b in the squared binomial. For example, in the trinomial 36 x 2 − 48 x + 16 {\displaystyle 36x^{2}-48x+16} 36x^{{2}}-48x+16, the last term is 16 {\displaystyle 16} 16. The square root of 16 {\displaystyle 16} 16 is 4 {\displaystyle 4} 4. So, the last term of this trinomial is a perfect square. Also, in the squared binomial, b = 4 {\displaystyle b=4} b=4
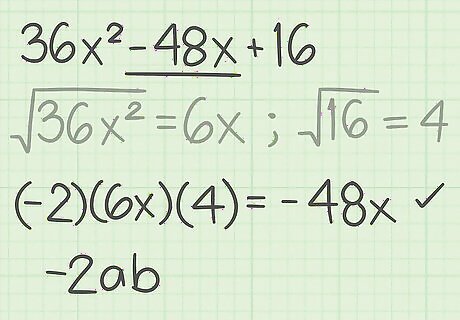
Determine whether the middle term follows the formula 2 a b {\displaystyle 2ab} 2ab or − 2 a b {\displaystyle -2ab} -2ab. That is, if you multiply the square roots of the first and last term of the trinomial, and then multiply that product by 2 or -2, the result will equal the middle term of the trinomial, if the trinomial is a perfect square. For example, if a = 6 x {\displaystyle a=6x} a=6x and b = 4 {\displaystyle b=4} b=4, then the middle term of the trinomial should follow the formula ( − 2 ) ( 6 x ) ( 4 ) {\displaystyle (-2)(6x)(4)} (-2)(6x)(4). Since ( − 2 ) ( 6 x ) ( 4 ) = − 48 x {\displaystyle (-2)(6x)(4)=-48x} (-2)(6x)(4)=-48x the middle term of the trinomial does follow the perfect square formula. Since the first and last terms of the trinomial followed the formula as well, you know that your trinomial is a perfect square.
Solving Sample Problems
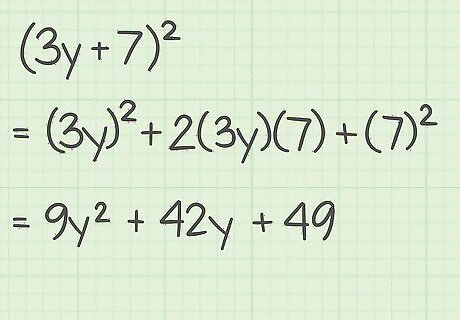
Expand the following expression. Use the perfect square identity rather than the FOIL method: ( 3 y + 7 ) 2 {\displaystyle (3y+7)^{2}} (3y+7)^{{2}}. Set up the formula ( a + b ) 2 = a 2 + 2 a b + b 2 {\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}} (a+b)^{{2}}=a^{{2}}+2ab+b^{{2}} and plug in the a {\displaystyle a} a and b {\displaystyle b} b values: ( 3 y + 7 ) 2 = ( 3 y ) 2 + 2 ( 3 y ) ( 7 ) + 7 2 {\displaystyle (3y+7)^{2}=(3y)^{2}+2(3y)(7)+7^{2}} (3y+7)^{{2}}=(3y)^{{2}}+2(3y)(7)+7^{{2}}. Square the first term: 9 y 2 + 2 ( 3 y ) ( 7 ) + 7 2 {\displaystyle 9y^{2}+2(3y)(7)+7^{2}} 9y^{{2}}+2(3y)(7)+7^{{2}}. Multiply the first and last term, and multiply the product by 2: 9 y 2 + 42 y + 7 2 {\displaystyle 9y^{2}+42y+7^{2}} 9y^{{2}}+42y+7^{{2}}. Square the last term: 9 y 2 + 42 y + 49 {\displaystyle 9y^{2}+42y+49} 9y^{{2}}+42y+49.
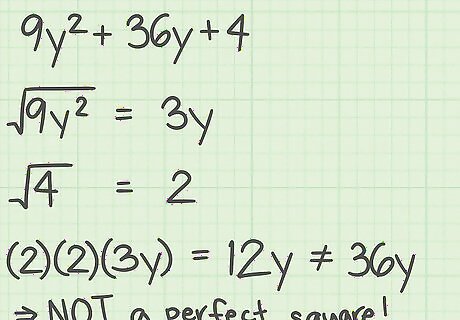
Consider the following trinomial. Determine whether it is a perfect square: 9 y 2 + 36 y + 4 {\displaystyle 9y^{2}+36y+4} 9y^{{2}}+36y+4. Recall the formula for a perfect square trinomial: ( a + b ) 2 = a 2 + 2 a b + b 2 {\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}} (a+b)^{{2}}=a^{{2}}+2ab+b^{{2}}. Determine whether the first term of the trinomial is a perfect square: 9 y 2 = 3 y {\displaystyle {\sqrt {9y^{2}}}=3y} {\sqrt {9y^{{2}}}}=3y. So, a = 3 y {\displaystyle a=3y} a=3y. Determine whether the last term of the trinomial is a perfect square: 4 = 2 {\displaystyle {\sqrt {4}}=2} {\sqrt {4}}=2. So, b = 2 {\displaystyle b=2} b=2. Determine whether the middle term of the trinomial follows the formula 2 a b {\displaystyle 2ab} 2ab: 36 y = ( 2 ) ( 3 y ) ( 2 ) {\displaystyle 36y=(2)(3y)(2)} 36y=(2)(3y)(2) 36 y = 12 y {\displaystyle 36y=12y} 36y=12ySince this is not true, the middle term does not follow the formula, and therefore the trinomial is not a perfect square.
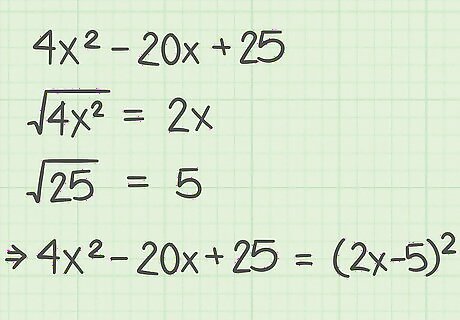
Factor the following trinomial. It factors into a squared binomial: 4 x 2 − 20 x + 25 {\displaystyle 4x^{2}-20x+25} 4x^{{2}}-20x+25. Since you know this factors into a squared binomial ( ( a − b ) 2 {\displaystyle (a-b)^{2}} (a-b)^{{2}}), you know that it follows the perfect square formula. Find the a {\displaystyle a} a term of the binomial, which is equal to the square root of the first term of the trinomial: 4 x 2 = 2 x {\displaystyle {\sqrt {4x^{2}}}=2x} {\sqrt {4x^{{2}}}}=2x. Find the b {\displaystyle b} b of the binomial, which is equal to the square root of the last term of the trinomial: 25 = 5 {\displaystyle {\sqrt {25}}=5} {\sqrt {25}}=5. Write the squared binomial. Since the second term of the trinomial is negative, you know that the second term of the binomial will also be negative: 4 x 2 − 20 x + 25 = ( 2 x − 5 ) 2 {\displaystyle 4x^{2}-20x+25=(2x-5)^{2}} 4x^{{2}}-20x+25=(2x-5)^{{2}}



















Comments
0 comment