views
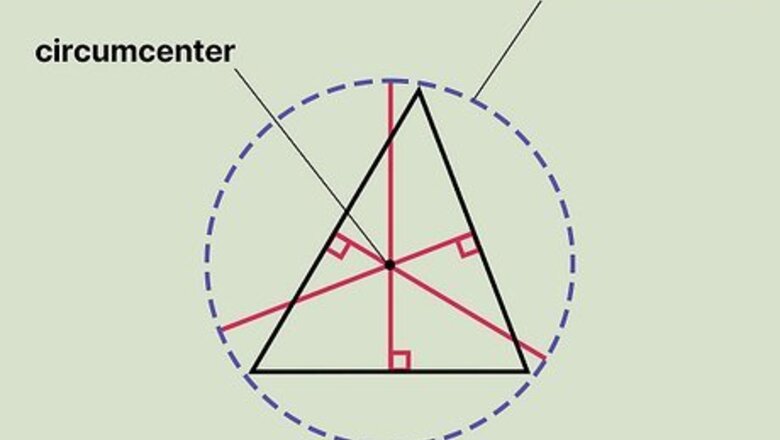
- Circumcenter is where the perpendicular lines at the midpoints of each triangle’s side intersect. Each vertex of the triangle is an equal distance from circumcenter.
- Find circumcenter using a triangle’s vertices and the mid-point and slope-intercept formulas.
- Alternatively, use the distance formula to find circumcenter.
- Draw the circumcenter on a triangle using a compass. Find the perpendicular, bisecting lines on the triangle’s sides and mark where they intersect.
What is the circumcenter?
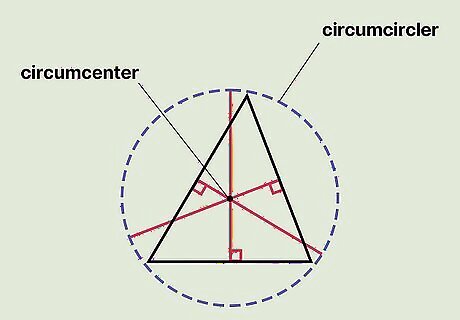
Circumcenter is where a triangle’s perpendicular, bisecting lines intersect. If you draw a line at the midpoint of each triangle’s side, you’ll have 3 perpendicular lines bisecting each side. These perpendicular lines all meet together at a point; this is the circumcenter. The circumcenter also forms the triangle’s circumcircle. It is the center of a circle, that when drawn, passes through each vertex of the triangle. The main principle behind the circumcenter is that each vertex on the triangle is an equal distance away from the circumcenter. On right triangles, the circumcenter is located at the midpoint of the hypotenuse, or the longest side of the triangle. On obtuse triangles, the circumcenter is located outside of the triangle. On acute triangles, the circumcenter is located inside the triangle.
Finding Circumcenter with the Midpoint Formula

Find the midpoints of the triangle using the vertices’ coordinates. Most math problems give you the (x, y) coordinates of each of the triangle’s vertices. The circumcenter is at the intersection of the perpendicular lines at the midpoint of the triangle’s sides. Because the distance from the circumcenter to each vertex is the same, you only need to find the midpoints of 2 sides. A triangle’s verticies are A = (-4, 2), B = (2, 4), and C = (4, -4). Use the midpoint formula: [(x1 + x2)/2,( y1 + y2)/2]. Plug in the coordinates for line AB: [(-4 + 2)/2, (2 + 4)/2]. Plug in the coordinates for line BC: [(2 + 4)/2, (4 + -4)/2]. Solve each midpoint: line AB's midpoint is (-1, 3) and line BC’s is (3, 0).
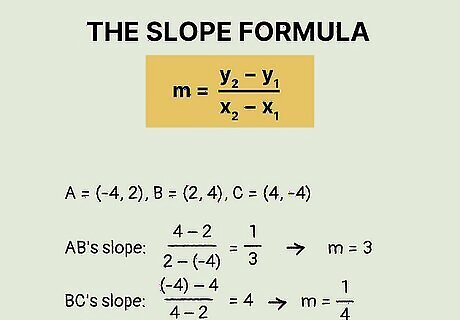
Calculate the slope of the 2 lines. The perpendicular lines at the triangle’s midpoints intersect to give you the circumcenter. So, calculate the slope of the lines to find out where they intersect. Because these lines are perpendicular, take the opposite reciprocal of the slope to find the perpendicular line’s slope. For example, a slope of 2/1 becomes -½. A triangles vertices are A = (-4, 2), B = (2, 4), and C = (4, -4). Use the slope formula: m = (y2 - y1) / (x2 - x1). Plug in the coordinates for line AB: m = (4 - 2) / (2 - -4). Plug in the coordinates for line BC: m = (-4 - 4) / (4 - 2). Solve each slope: line AB’s slope is m = ⅓ and line BC’s is m = -4. Take the opposite reciprocal of the slope: Flip AB’s slope to 1/(⅓) and change the sign. The perpendicular slope is m = -3. BC’s perpendicular slope is m = ¼.
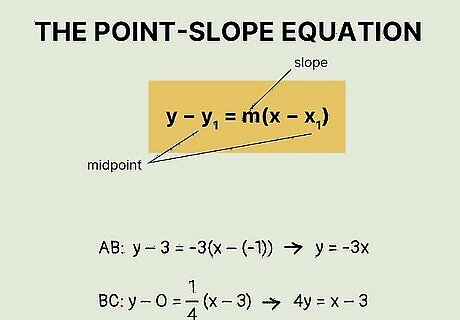
Solve each line’s point-slope equation to find the y-intercept. With your slopes identified for the perpendicular lines, use the slope-intercept formula of y - y1 = m(x - x1) to find the entire slope equation. Use the point-slope equation: y - y1 = m(x - x1) Plug in the midpoint and slope for line AB: y - 3 = -3(x - -1). Plug in the midpoint and slope for line BC: y - 0 = ¼(x - 3). Solve and simplify each equation: line AB’s is y = -3x. Line BC’s is y = ¼x - ¾ (or 4y = x - 3 if you get rid of the fractions).
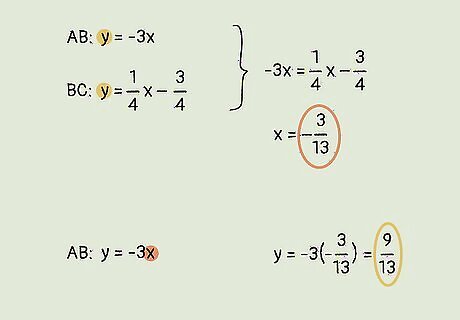
Set the equations equal to each other to find circumcenter. Use substitution to find where the 2 perpendicular lines intersect. Insert line AB’s y-value into line BC’s point-slope equation. This gives you an x-value. Then, plug the x-value into either point-slope equation to find the y-coordinate. Put the x and y values together to get the circumcenter’s coordinates! Substitute line AB’s point-slope equation into line BC’s equation: (-3x) = ¼x - ¾. Solve for x: x = -3/13. Plug x into either equation: y = -3(-3/13) with y = 9/13. So, the circumcenter is located at (-3/13, 9/13).
Finding Circumcenter with the Distance Formula
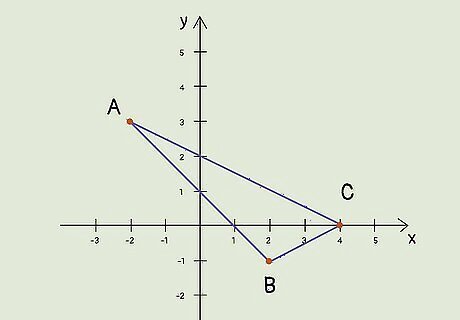
Use the distance formula to set 2 vertices equal to each other. Each vertex on the triangle is the same distance away from the circumcenter. If the circumcenter is O and the triangle’s vertices are A, B, and C, the distance between A to O is the same as B to O and C to O. So, set AO and BO equal to each other, as well as BO and CO, using the distance formula. A triangle’s vertices are A = (−2, 3), B = (2, −1), and C = (4, 0). Use a simplified distance formula: (x2 - x1) + (y2 - y1). Set A and B equal to each other: (-2 - x) + (3 - y) = (2 - x) + (-1 - y). Set B and C equal to each other: (2 - x) + (-1 - y) = (4 - x) + (0 - y).
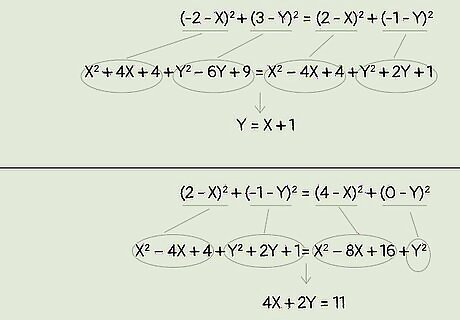
Solve the distance equations. Use the FOIL method (First, Outer, Inner, Last) to multiply the squared expressions together (i.e. (-2-x) in the example above). Then, simplify the expression by adding or subtracting the x, y, and numerical values together. Use FOIL to solve each equation. For AO = BO: x + 4x + 4 + y − 6y + 9 = x − 4x + 4 + y + 2y +1 For BO = CO: x − 4x + 4 + y + 2y + 1= x − 8x + 16 + y Solve and simplify each equation: AO = BO results in y = x + 1. Solving BO = CO results in 4x + 2y = 11.
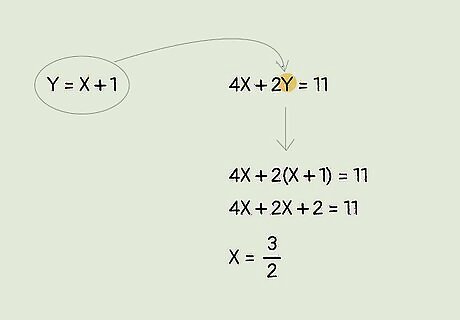
Substitute 1 equation into the 2nd to get the circumcenter’s x-value. To find the x-coordinate of the circumcenter, insert the first equation's y-value in the second equation. Then, solve for x. Substitute AO = BO’s equation into BO = CO: 4x + 2(x + 1) = 11. Expand the equation: 4x + 2x +2 = 11. Solve for x: x = 3/2.
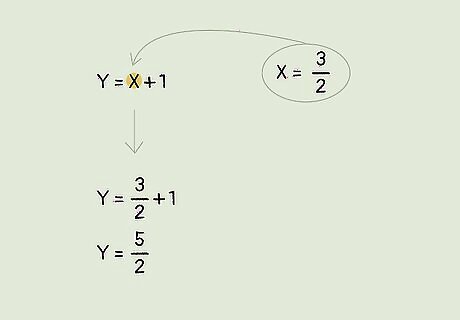
Insert the x-value in one of the equations to find the y-coordinate. Now that you know what the circumcenter’s x-coordinate is, solve for its y-coordinate. Just substitute x into one of the equations and solve. Then, put the x and y-values together to get the circumcenter’s coordinates! Insert x into one of the equations: y = (3/2) + 1. Solve for y: y = 5/2. So, the circumcenter’s coordinates are (3/2, 5/2).
Drawing the Circumcenter with a Compass
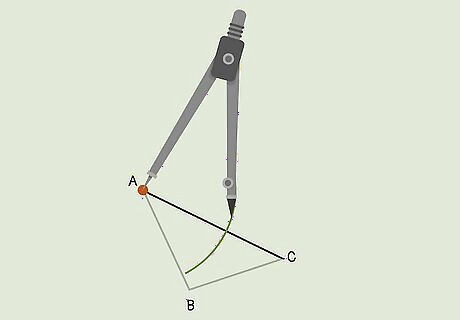
Use a compass to draw an arc through one of the triangle’s sides. Choose a side of the triangle and place the compass point on one of the line’s vertices; these are the points where 2 lines meet. Open the compass up so it’s a little more than half as long as the line segment. With the point in place, draw one continuous arc spanning below the triangle’s side, through it, and above it.
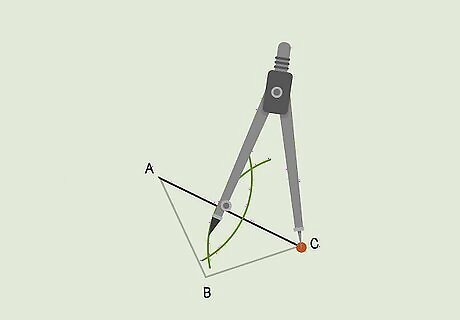
Place the compass on the line’s other vertex and draw an arc. Using the same triangle side you chose, move the compass point to the line’s other vertex. Follow the same steps as above to draw an arc above and below this side, too.
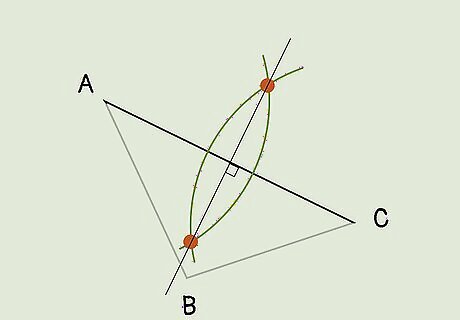
Use a ruler to draw a line through the points where the arcs intersect. With your 2 arcs drawn, you’ll see 2 points where they meet. Just take out a ruler and draw a straight line through these points, taking the line through the triangle’s side. This gives you the midpoint of this triangle line and the perpendicular, bisecting line.
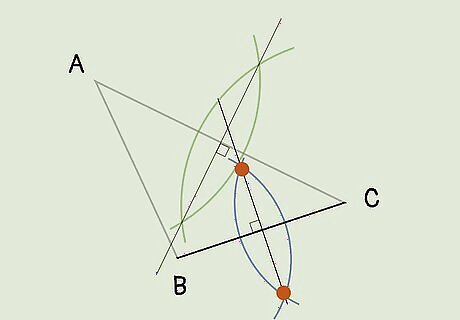
Follow the same steps for one of the triangle’s other sides. Place the compass point at the vertex of one of the other triangle sides. Adjust the compass so it’s open to about half the size of the line segment. Draw an arc, then move the compass to the side’s other vertex. Make the other arc line, then draw a straight line through the intersecting points.
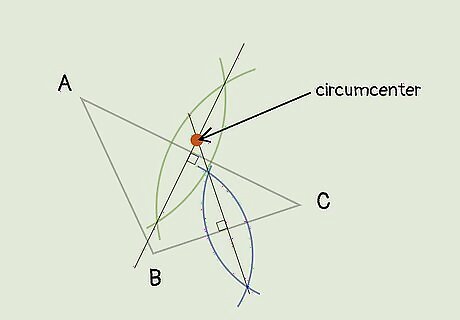
Find the circumcenter by marking where the 2 lines intersect. With your 2 perpendicular, bisecting lines drawn, simply mark where they intersect. Depending on the type of triangle you have, the circumcenter might be in the triangle, on one of its sides, or outside of the triangle. If you want, find the perpendicular line of the 3rd triangle side, too. You’ll see that its perpendicular, bisecting line also passes through the circumcenter.
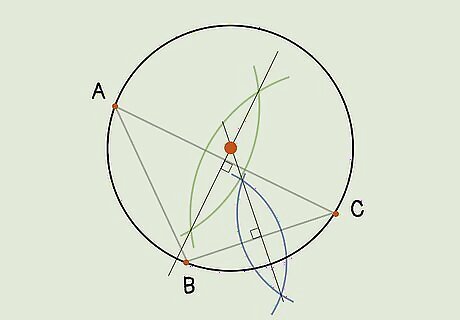
Use the compass to draw the circumcircle around the triangle. Place the compass point at the circumcenter. Then, adjust the compass so the pencil reaches one of the triangle’s vertices. Draw the circle. As you go around the triangle, you’ll notice that the edges of the circle just touch each point of the triangle. This is because the triangle’s vertices are equidistant from the circumcenter.


















Comments
0 comment