
views
Determining Which Approach to Use

Look at how complex the divisor is. How complicated the divisor (the polynomial you’re dividing by) is compared to the dividend (the polynomial you’re dividing into) determines which approach is best. If the divisor is a monomial (single-term polynomial), either a variable with a coefficient, or a constant (a number without a variable following it), you can probably factor the dividend and cancel out one of the resulting factors and the divisor. See “Factoring the Dividend” for instructions and examples. If the divisor is a binomial (two-term polynomial), you may be able to factor the dividend and cancel out one of the resulting factors and the divisor. If the divisor is a trinomial (three-term polynomial), you may be able to factor both the dividend and the divisor, cancel out the common factor, and then either factor out the dividend further or use long division. If the divisor is a polynomial with more than three factors, you will probably have to use long division. See “Using Long Polynomial Division” for instructions and examples.
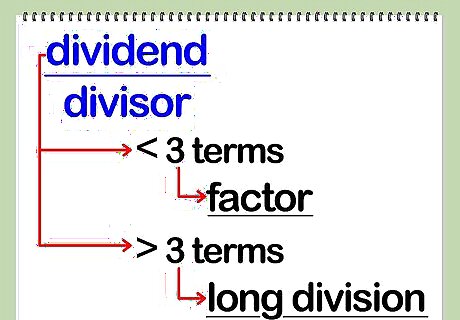
Look at how complex the dividend is. If looking at the divisor polynomial of the equation doesn’t tell you whether you should try to factor the dividend, look at the dividend itself. If the dividend has three terms or fewer, you can probably factor it and cancel out the divisor. If the dividend has more than three terms, you will probably have to divide the divisor into it by using long division.
Factoring the Dividend[4] X Research source
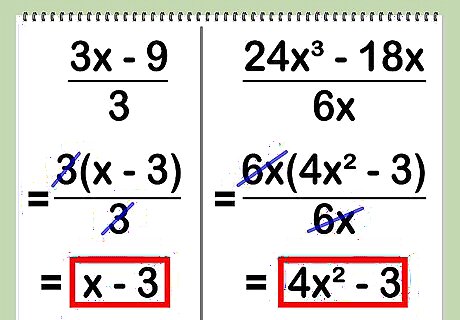
Look to see if all the terms in the dividend contain a common factor with the divisor. If this is the case, you can factor it out and probably cancel out the divisor. If you’re dividing the binomial 3x – 9 by 3, you can factor 3 out of both terms of the binomial, making it 3(x – 3). You can then cancel out the divisor of 3, leaving a quotient of x – 3. If you’re dividing the binomial 24x - 18x by 6x, you can factor 6x out of both terms of the binomial, making it 6x(4x - 3). You can the cancel out the divisor of 6x, leaving a quotient of 4x - 3.
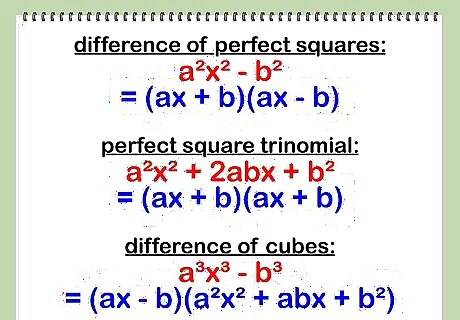
Look for special patterns in the dividend that tell you it can be factored. Certain polynomials display terms that tell you they can be factored. If one of those factors matches the divisor, you can cancel it out, leaving the remaining factor as the quotient. Here are some patterns to look for: Difference of perfect squares. This is a binomial of the form ‘’a x - b ’’, where the values of ‘’a ’’ and ‘’b ’’ are perfect squares. This binomial factors into two binomials (ax + b)(ax – b), where a and b are the square roots of the coefficient and constant of the earlier binomial. Perfect square trinomial. This trinomial is in the form ax + 2abx + b . It factors to (ax + b)(ax + b), which may also be written (ax + b). If the sign in front of the second term is a minus sign, the binomial factors will be in the form (ax – b)(ax – b). Sum or difference of cubes. This is a binomial of the form ax + b or ax - b, where the values of ‘’a ’’ and ‘’b ’’ are perfect cubes. This binomial factors into a binomial and a trinomial. A sum of cubes factors down to (ax + b)(ax - abx + b). A difference of cubes factors down to (ax - b)(ax + abx + b).

Use trial and error to factor the dividend. If you don’t see a discernible pattern in the dividend to tell you how to factor it, you can try several possible factoring combinations. You can do this by looking first at the constant and finding several factors for it, then at the coefficient of the middle term. For example, if the dividend is x - 3x – 10, you would look at the factors of 10 and use the 3 to help determine which factor pair is correct. The number 10 can be broken into factors of 1 and 10 or 2 and 5. Because the sign in front of 10 is negative, one of the factor binomials has to have a negative number in front of its constant. The number 3 is the difference between 2 and 5, so these must be the constants of the factor binomials. Because the sign in front of the 3 is negative, the binomial with the 5 must be the one with the negative number. The binomial factors are thus (x – 5)(x + 2). If the divisor is one of these two factors, that factor can be canceled out, and the remaining factor is the quotient.
Using Long Polynomial Division[6] X Research source
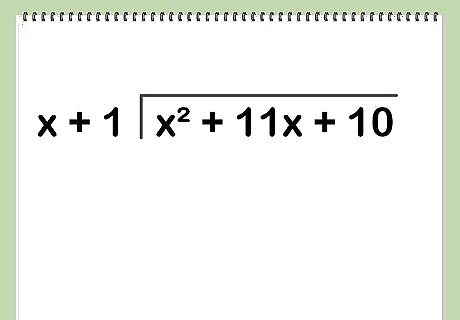
Set up the division. You write out the long division of polynomials the same as you do for dividing numbers. The dividend goes under the long division bar, while the divisor goes to the left. If you’re dividing x + 11 x + 10 by x +1, x + 11 x + 10 goes under the bar, while x + 1 goes to the left.
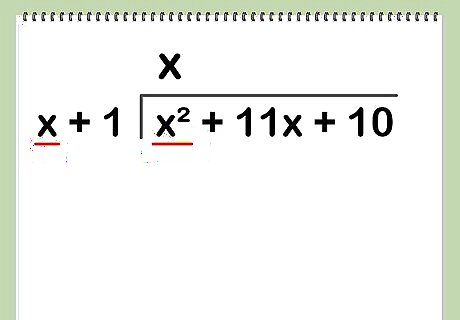
Divide the first term of the divisor into the first term of the dividend. The result of this division goes on top of the division bar. For our example, dividing x, the first term of the dividend, by x, the first term of the divisor yields x. You would write an x on the top of the division bar, over the x.
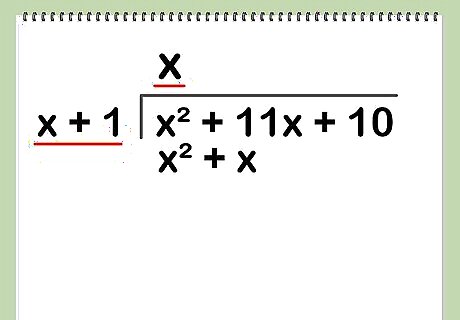
Multiply the x in the quotient position by the divisor. Write the result of the multiplication under the leftmost terms of the dividend. Continuing with our example, multiplying x + 1 by x produces x + x. You would write this under the first two terms of the dividend.
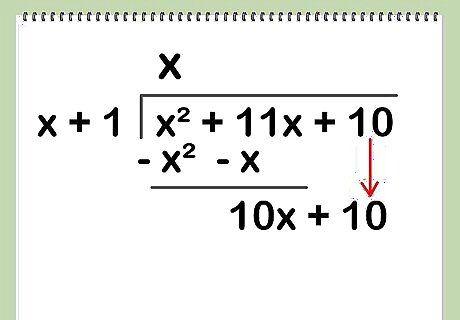
Subtract from the dividend. To do so, first reverse the signs of the product of the multiplication. After subtracting, bring down the remaining terms of the dividend. Reversing the signs of x + x gives - x - x. Subtracting this from the first two terms of the dividend leaves 10x. After bringing down the remaining term of the dividend, you have 10x + 10 as the interim quotient to continue the division process with.
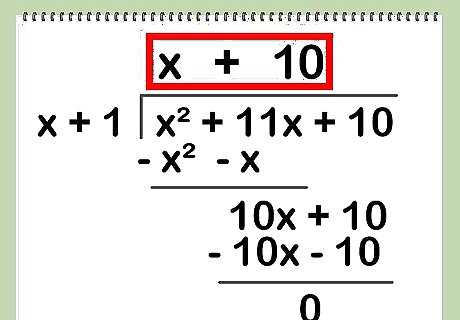
Repeat the previous three steps on the interim quotient. You’ll again divide the first term of the divisor into that of the interim quotient, write that result on top of the division bar after the first term of the quotient, multiply the result by the divisor, and then calculate what to subtract from the interim quotient. Because x goes into 10x 10 times, you would write “+ 10” after the x in the quotient position on the division bar. Multiplying x +1 by 10 gives 10x + 10. You write this under the interim quotient and reverse the signs for the subtraction, making -10x – 10. When you perform the subtraction, you have a remainder of 0. Thus, dividing x + 11 x + 10 by x +1 produces a quotient of x + 10. (You could have gotten the same result by factoring, but this example was chosen to keep the division fairly simple.)



















Comments
0 comment