Using Linear Equations to Find Ordered Pairs (with Practice Problems)

• Use the slope-intercept equation ${\displaystyle y=mx+b}$ to find ordered pairs.
• Substitute any value for ${\displaystyle x}$ and solve for ${\displaystyle y}$ to find the ordered pair ${\displaystyle (x,y)}$.
• When plotting an ordered pair on a graph, the first number represents horizontal lines and the second is vertical lines.

What is an ordered pair?

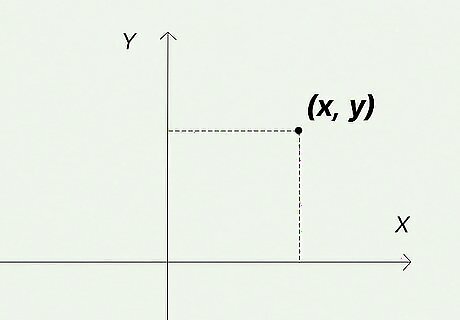
An ordered pair is a set of numbers that tells you the location of a point on a coordinate plane. The ordered pair is always expressed exactly the same way: ( x , y ) {\displaystyle (x,y)} (x,y). The first number represents the x {\displaystyle x} x coordinate on the plane while the second number represents the y {\displaystyle y} y coordinate. The x {\displaystyle x} x-coordinate tells you how far away the point is horizontally from the y {\displaystyle y} y-axis. The y {\displaystyle y} y-coordinate tells you how far away the point is vertically from the x {\displaystyle x} x-axis.

Using Linear Equations

Start with a standard linear equation A x + B y = C {\displaystyle Ax+By=C} Ax+By=C. In this standard linear equation, x {\displaystyle x} x represents the x {\displaystyle x} x coordinate of a point and y {\displaystyle y} y represents the y {\displaystyle y} y coordinate of that same point. So you have two variables you'll need to find—your ordered pair. For example, the equation 5 x + y = 1 {\displaystyle 5x+y=1} {\displaystyle 5x+y=1} is a linear equation. If you see a " − {\displaystyle -} -" instead of a " + {\displaystyle +} +", that means the y {\displaystyle y} y coordinate is negative. If you're working on a problem that asks you to determine whether a given ordered pair is a solution to the equation provided, you'd just plug in the numbers for x {\displaystyle x} x and y {\displaystyle y} y and see if they worked.

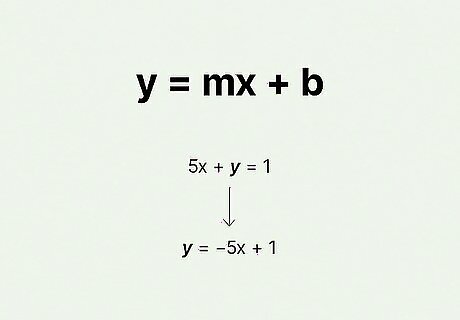
Convert the standard linear equation to y = m x + b {\displaystyle y=mx+b} y=mx+b to find y {\displaystyle y} y. Sometimes, you'll have a problem that asks you to find ordered pairs that are solutions for the equation. The easiest way to do these problems is to get one of the variables on the other side of the equation so you can solve for it. Try working through it with 5 x + y = 1 {\displaystyle 5x+y=1} {\displaystyle 5x+y=1}: Start by subtracting 5 x {\displaystyle 5x} 5x from each side to get the y {\displaystyle y} y by itself: 5 x + y − 5 x = 1 − 5 x {\displaystyle 5x+y-5x=1-5x} {\displaystyle 5x+y-5x=1-5x} Simplify: y = 1 − 5 x {\displaystyle y=1-5x} {\displaystyle y=1-5x} Almost there! Swap the order of the expression so it matches the slope-intercept form: y = − 5 x + 1 {\displaystyle y=-5x+1} {\displaystyle y=-5x+1} You might recognize this as slope-intercept form. It's also referred to as function form.

Choose any value for x {\displaystyle x} x in your equation. You might be thinking, "Really? I just choose any number?" Recall that there are infinite points on a line. That means that for any x {\displaystyle x} x, there will be a y {\displaystyle y} y. So yes, unless the problem specifies the numbers you should use for x {\displaystyle x} x, you can choose literally any number. Don't make this too hard on yourself! Choose a simple number, like 1 {\displaystyle 1} 1. For example, if you're working with y = 1 − 5 x {\displaystyle y=1-5x} {\displaystyle y=1-5x}, you could replace the x {\displaystyle x} x with 1 {\displaystyle 1} 1 and get y = 1 − 5 ( 1 ) {\displaystyle y=1-5(1)} {\displaystyle y=1-5(1)}.

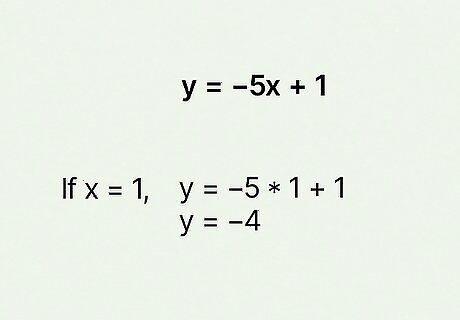
Solve your equation for y {\displaystyle y} y. Now you have all numbers on one side of the equation, so you can easily solve it like any other basic equation. Just remember to pay attention to your order of operations! For example, if you chose 1 {\displaystyle 1} 1 for the x {\displaystyle x} x value in y = 1 − 5 x {\displaystyle y=1-5x} {\displaystyle y=1-5x}, you would have y = 1 − 5 ( 1 ) = 1 − 5 = − 4 {\displaystyle y=1-5(1)=1-5=-4} {\displaystyle y=1-5(1)=1-5=-4}. So y = − 4 {\displaystyle y=-4} y=-4.

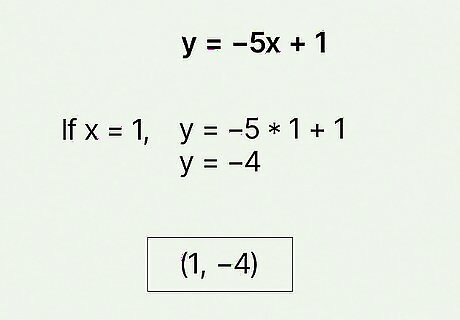
Write your ordered pair as ( x , y ) {\displaystyle (x,y)} (x,y) using the value for x {\displaystyle x} x that you chose. The y {\displaystyle y} y value that you found is the y {\displaystyle y} y coordinate in your ordered pair. It goes second, and the number you chose for x {\displaystyle x} x goes first. To continue the previous example, your ordered pair would be ( 1 , − 4 ) {\displaystyle (1,-4)} {\displaystyle (1,-4)}. You might have problems that ask you to find several ordered pairs that are solutions to the linear equation. Find the other ordered pairs the same way you did with the first, choosing a new value for x {\displaystyle x} x and then solving for y {\displaystyle y} y.

Plotting on a Graph

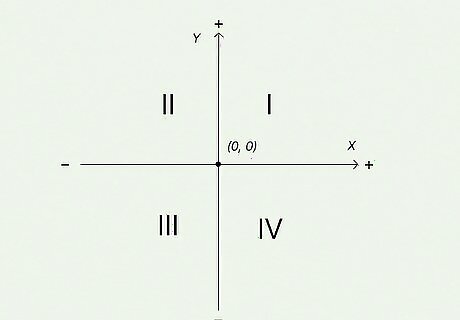
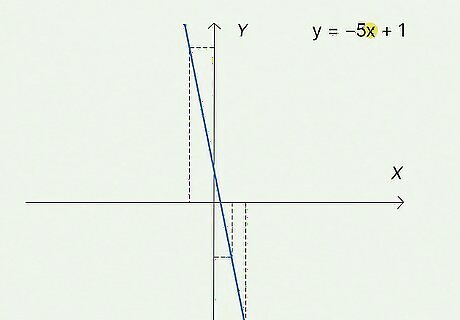
Start at the origin of the graph. A standard rectangular coordinate plane is bisected horizontally by the x {\displaystyle x} x axis and vertically by the y {\displaystyle y} y axis. The point in the center of the plane where the two axes intersect is the origin. The coordinates of the origin are ( 0 , 0 ) {\displaystyle (0,0)} (0,0). The axes divide the graph into four quadrants, each of which is labeled by Roman numerals: Quadrant I: the upper-right quadrant of the plane; all points in this quadrant have positive x {\displaystyle x} x coordinates and positive y {\displaystyle y} y coordinates ( + , + ) {\displaystyle (+,+)} {\displaystyle (+,+)} Quadrant II: the upper-left quadrant of the plane; all points in this quadrant have negative x {\displaystyle x} x coordinates and positive y {\displaystyle y} y coordinates ( + , − ) {\displaystyle (+,-)} {\displaystyle (+,-)} Quadrant III: the lower-left quadrant of the plane; all points in this quadrant have negative x {\displaystyle x} x coordinates and negative y {\displaystyle y} y coordinates ( − , − ) {\displaystyle (-,-)} {\displaystyle (-,-)} Quadrant IV: the lower-right quadrant of the plane; all points in this quadrant have positive x {\displaystyle x} x coordinates and negative y {\displaystyle y} y coordinates ( + , − ) {\displaystyle (+,-)} {\displaystyle (+,-)}

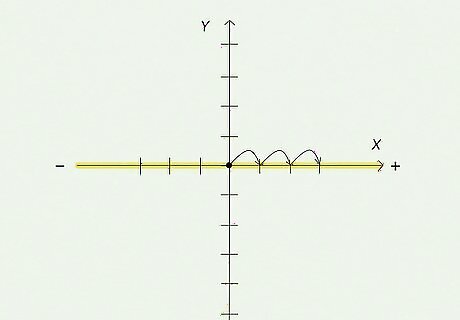
Move horizontally from the origin to place the x {\displaystyle x} x coordinate. The first number of the ordered pair represents your point's x {\displaystyle x} x coordinate. Just count the lines from the y {\displaystyle y} y axis to the first number in your ordered pair. The sign in front of the x {\displaystyle x} x coordinate tells you which direction to go. If the x {\displaystyle x} x coordinate is positive, you'll go right from the y {\displaystyle y} y axis. For negative numbers, you'll go left. You can also think of right as east and left as west. This is helpful with word problems that involve directions.

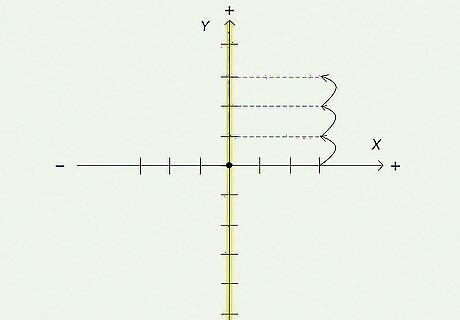
Move vertically from the x {\displaystyle x} x coordinate to locate the y {\displaystyle y} y coordinate. The second number of the ordered pair is your point's y {\displaystyle y} y coordinate. Stay on the line you've found for your x {\displaystyle x} x and count the lines from the x {\displaystyle x} x axis to find your y {\displaystyle y} y coordinate. If the y {\displaystyle y} y coordinate is positive, you'll go up from the x {\displaystyle x} x axis. A negative y {\displaystyle y} y coordinate, on the other hand, will be down or below the x {\displaystyle x} x axis. In word problems that use cardinal directions, positive numbers are north and negative numbers are south.

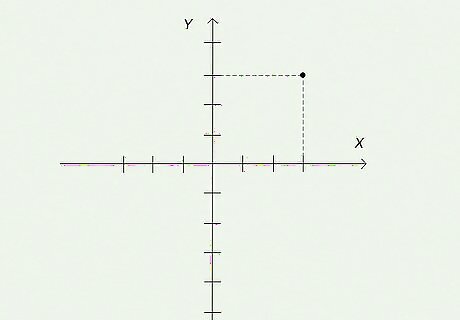
Plot your point at the intersection of the x {\displaystyle x} x coordinate and the y {\displaystyle y} y coordinate. The intersection of those grid lines is the point represented by the ordered pair you have. Simple, right? Make a good-sized dot there so you'll be able to find it easily. If you have other ordered pairs, continue plotting those points as well. For example, you might have a problem where you're supposed to plot 3 points and then draw a line connecting them.

Practice Problems

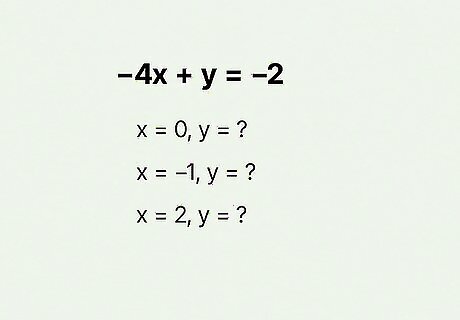
Equation forms problem Find three solutions to the equation − 4 x + y = − 2 {\displaystyle -4x+y=-2} {\displaystyle -4x+y=-2}, using 0 {\displaystyle 0} {\displaystyle 0}, − 1 {\displaystyle -1} -1, and 2 {\displaystyle 2} {\displaystyle 2} for x {\displaystyle x} x. Hint: Convert the equation from standard form to slope-intercept or function form ( y = m x + b {\displaystyle y=mx+b} y=mx+b), then solve for y {\displaystyle y} y.

Directions problem Braden lives 2 {\displaystyle 2} {\displaystyle 2} blocks north and 1 {\displaystyle 1} 1 block east of school. Riley lives 3 {\displaystyle 3} 3 blocks south and 2 {\displaystyle 2} {\displaystyle 2} blocks west of school. Write the ordered pairs that represent each house. Hint: In this problem, assume that "school" is the origin of the coordinate plane and each block is one line.

Word problem Ms. Frizzle wants to take her class to a special show at the local Science Museum. Tickets for the special show are $5 each, plus a $2 fee for each ticket. Determine the total cost for 18 students. Write your answer as an ordered pair. Hint: Let x {\displaystyle x} x represent the number of tickets so you can solve for y {\displaystyle y} y, the total cost.

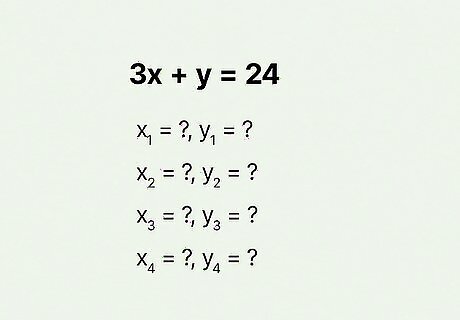
Multiple solutions problem Find four solutions for 3 x + y = 24 {\displaystyle 3x+y=24} {\displaystyle 3x+y=24}. Write your answers as ordered pairs. Hint: Remember that you can choose whatever value you want for x {\displaystyle x} x.

Practice Problem Solutions

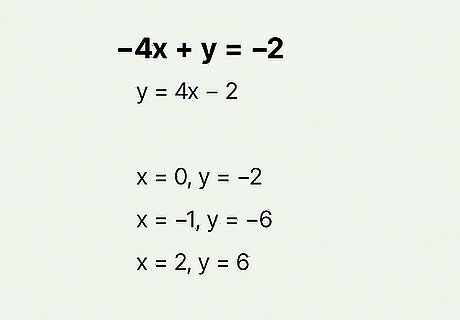
The ordered pairs are ( , − 2 ) {\displaystyle (0,-2)} {\displaystyle (0,-2)}, ( − 1 , − 6 ) {\displaystyle (-1,-6)} {\displaystyle (-1,-6)}, and ( 2 , 6 ) {\displaystyle (2,6)} {\displaystyle (2,6)}. Start by converting the equation − 4 x + y = − 2 {\displaystyle -4x+y=-2} {\displaystyle -4x+y=-2} by adding 4 x {\displaystyle 4x} 4x to both sides, then simplify to get y = − 2 + 4 x {\displaystyle y=-2+4x} {\displaystyle y=-2+4x}. Swap the order so it matches the slope-intercept form, and you have y = 4 x − 2 {\displaystyle y=4x-2} {\displaystyle y=4x-2}. Now all you have to do is solve each of the three equations: For x {\displaystyle x} x of 0 {\displaystyle 0} {\displaystyle 0} : y = 4 ( 0 ) − 2 = 0 − 2 = − 2 {\displaystyle y=4(0)-2=0-2=-2} {\displaystyle y=4(0)-2=0-2=-2}, so your ordered pair is ( 0 , − 2 ) {\displaystyle (0,-2)} {\displaystyle (0,-2)}. For x {\displaystyle x} x of − 1 {\displaystyle -1} -1 : y = 4 ( − 1 ) − 2 = − 4 − 2 = − 6 {\displaystyle y=4(-1)-2=-4-2=-6} {\displaystyle y=4(-1)-2=-4-2=-6}, so your ordered pair is ( − 1 , − 6 ) {\displaystyle (-1,-6)} {\displaystyle (-1,-6)}. For x {\displaystyle x} x of 2 {\displaystyle 2} {\displaystyle 2} : y = 4 ( 2 ) − 2 = 8 − 2 = 6 {\displaystyle y=4(2)-2=8-2=6} {\displaystyle y=4(2)-2=8-2=6}, so your ordered pair is ( 2 , 6 ) {\displaystyle (2,6)} {\displaystyle (2,6)}.

The ordered pairs are ( 1 , 2 ) {\displaystyle (1,2)} {\displaystyle (1,2)} and ( − 2 , − 3 ) {\displaystyle (-2,-3)} {\displaystyle (-2,-3)}. This question asks you to think of where a point might be on a coordinate plane. Start by sketching out your axes and labeling your quadrants. Then, all you have to do is find the two houses: Braden lives north and east of school. North is up (vertical) and east is to the right (horizontal)—that means you're in quadrant I, where both numbers are positive. Now, all you've gotta do is plug in the numbers you were given to get ( 1 , 2 ) {\displaystyle (1,2)} {\displaystyle (1,2)} as your ordered pair. Riley lives south and west of school. South is down (vertical) and west is to the left (horizontal)—that means you're in quadrant III, where both numbers are negative. Plug in the numbers provided in the problem, and you find your ordered pair is − 2 , − 3 {\displaystyle -2,-3} {\displaystyle -2,-3}.

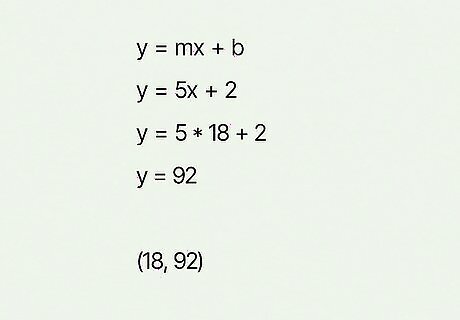
The total cost is $ 92 {\displaystyle \$92} {\displaystyle \$92}, or ( 18 , 92 ) {\displaystyle (18,92)} {\displaystyle (18,92)}. Since the total cost is y {\displaystyle y} y, use the equation that lets you solve for y {\displaystyle y} y, which is y = m x + b {\displaystyle y=mx+b} y=mx+b. Since each ticket costs $ 5 {\displaystyle \$5} {\displaystyle \$5}, you'll use 5 x {\displaystyle 5x} 5x, then add the $ 2 {\displaystyle \$2} {\displaystyle \$2} fee to fill out the equation: y = 5 x + 2 {\displaystyle y=5x+2} {\displaystyle y=5x+2}. Since you were told to compute the total cost for 18 {\displaystyle 18} 18 students, you'll plug in 18 {\displaystyle 18} 18 for x {\displaystyle x} x: y = 5 ( 18 ) + 2 {\displaystyle y=5(18)+2} {\displaystyle y=5(18)+2}. Now, solve the equation: y = 90 + 2 = 92 {\displaystyle y=90+2=92} {\displaystyle y=90+2=92}. The total cost for 18 {\displaystyle 18} 18 students is $ 92 {\displaystyle \$92} {\displaystyle \$92}. Then, since 18 {\displaystyle 18} 18 was your x {\displaystyle x} x value, it will be the first number of your ordered pair. As the y {\displaystyle y} y value, 92 {\displaystyle 92} {\displaystyle 92} will be the second number.

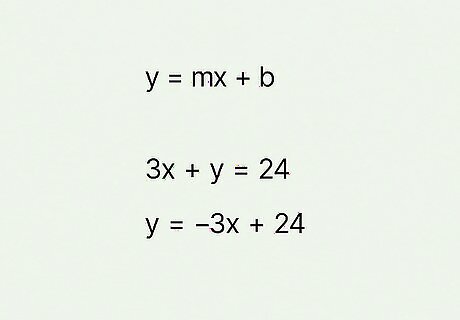
Your answers will vary depending on what values you chose for x {\displaystyle x} x. Your first step is to get the equation into slope-intercept or function form so you can solve for y {\displaystyle y} y. Start by subtracting 3 x {\displaystyle 3x} 3x from both sides: 3 x + y − 3 x = 24 − 3 x {\displaystyle 3x+y-3x=24-3x} {\displaystyle 3x+y-3x=24-3x}. Then, simplify: y = 24 − 3 x {\displaystyle y=24-3x} {\displaystyle y=24-3x}. Finally, adjust the order so it matches the formula y = m x + b {\displaystyle y=mx+b} y=mx+b: y = − 3 x + 24 {\displaystyle y=-3x+24} {\displaystyle y=-3x+24}. Now you're ready to solve! Let's go through a couple with different values of x {\displaystyle x} x so you can make sure your answers are on the right track: Assume you chose 1 {\displaystyle 1} 1 as one of your values of x {\displaystyle x} x. Your work would look like this: y = − 3 ( 1 ) + 24 = − 3 + 24 = 21 {\displaystyle y=-3(1)+24=-3+24=21} {\displaystyle y=-3(1)+24=-3+24=21}. Ordered pair: ( 1 , 21 ) {\displaystyle (1,21)} {\displaystyle (1,21)} What if you chose − 2 {\displaystyle -2} -2? You'd get y = − 3 ( − 2 ) + 24 = 6 + 24 = 30 {\displaystyle y=-3(-2)+24=6+24=30} {\displaystyle y=-3(-2)+24=6+24=30}. Ordered pair: ( − 2 , 30 ) {\displaystyle (-2,30)} {\displaystyle (-2,30)}.