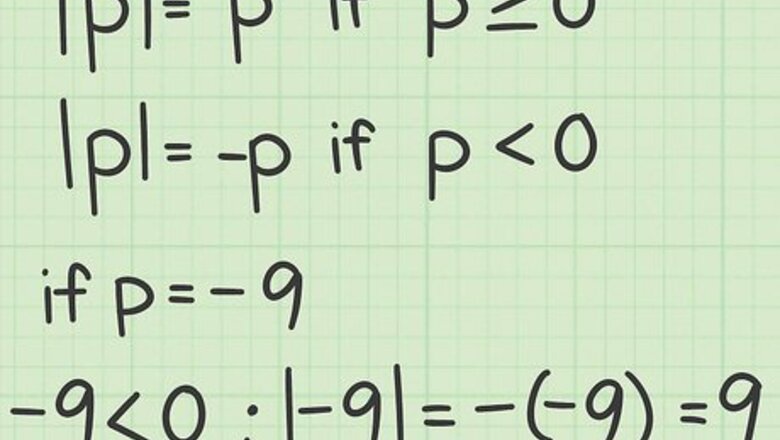
views
x
{\displaystyle x}
is denoted as
|
x
|
{\displaystyle |x|}
, and it is always positive, except for zero, which is neither positive nor negative. An absolute value equation is solved using the same rules as any other algebraic equation; however, this type of equation has two potential results, derived from a positive equation and a negative equation.
Setting up the Problem
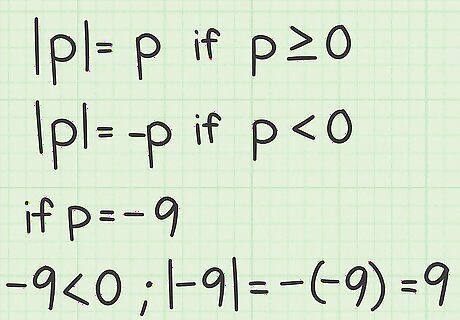
Understand the mathematical definition of absolute value. The definition states that | p | = { p if p ≥ 0 − p if p < 0 {\displaystyle |p|={\begin{cases}p&{\text{if }}p\geq 0\\-p&{\text{if }}p<0\end{cases}}} |p|={\begin{cases}p&{\text{if }}p\geq 0\\-p&{\text{if }}p.This formula tells you that if a number p {\displaystyle p} p is positive, the absolute value is simply p {\displaystyle p} p. If a number p {\displaystyle p} p is negative, then the absolute value is the negative value of − p {\displaystyle -p} -p. Since two negatives make a positive, the absolute value of − p {\displaystyle -p} -p is therefore positive. For example, |9| = 9; |-9| = -(-9) = 9.
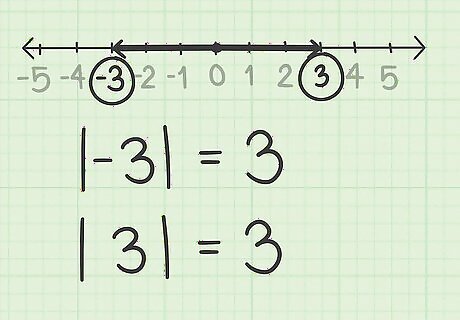
Understand what an absolute value represents. The absolute value of a number represents how far away from 0 the number is on a number line. Absolute value is denoted by bars surrounding the term or terms ( | x | {\displaystyle |x|} |x|). The absolute value of a number is always positive. For example, | − 3 | = 3 {\displaystyle |-3|=3} |-3|=3 and | 3 | = 3 {\displaystyle |3|=3} |3|=3. Both -3 and 3 are three numbers away from 0.
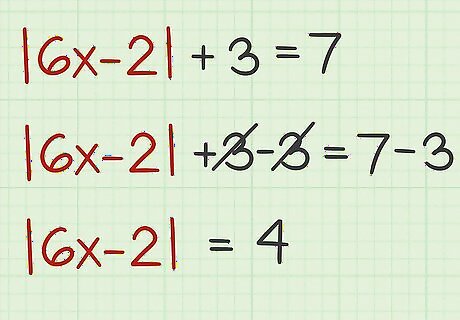
Isolate the absolute value term(s) in your equation. The absolute value should be on one side of the equation. Any numbers that are not included inside the absolute value symbols should be moved to the other side of the equation. Note that an absolute value can never equal a negative number, so if, after isolating the absolute value, your absolute value equals a negative number, the equation has no solution. For example, if your equation is | 6 x − 2 | + 3 = 7 {\displaystyle |6x-2|+3=7} |6x-2|+3=7, then subtract three from both sides of the equation to isolate the absolute value: | 6 x − 2 | + 3 = 7 {\displaystyle |6x-2|+3=7} |6x-2|+3=7 | 6 x − 2 | + 3 − 3 = 7 − 3 {\displaystyle |6x-2|+3-3=7-3} |6x-2|+3-3=7-3 | 6 x − 2 | = 4 {\displaystyle |6x-2|=4} |6x-2|=4
Calculating the Values
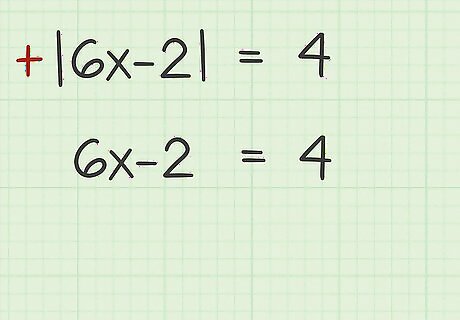
Set up the equation for the positive value. An equation involving absolute value will have two possible solutions. To set up the positive equation, simply remove the absolute value bars, and solve the equation as normal. For example, the positive equation for | 6 x − 2 | = 4 {\displaystyle |6x-2|=4} |6x-2|=4 is 6 x − 2 = 4 {\displaystyle 6x-2=4} 6x-2=4.
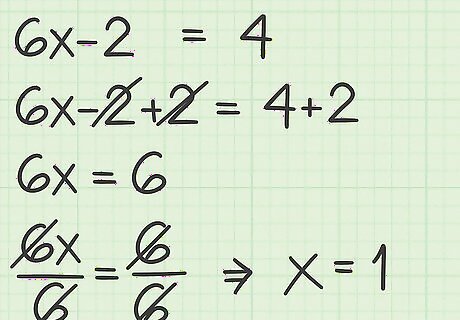
Solve the positive equation. To do this, use algebra to solve for the variable. This will give you the first possible solution to the equation. For example: 6 x − 2 = 4 {\displaystyle 6x-2=4} 6x-2=4 6 x − 2 + 2 = 4 + 2 {\displaystyle 6x-2+2=4+2} 6x-2+2=4+2 6 x = 6 {\displaystyle 6x=6} 6x=6 6 x 6 = 6 6 {\displaystyle {\frac {6x}{6}}={\frac {6}{6}}} {\frac {6x}{6}}={\frac {6}{6}} x = 1 {\displaystyle x=1} x=1
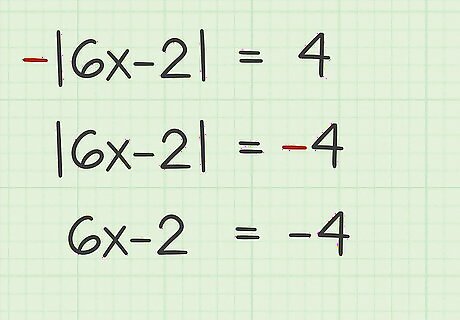
Set up the equation for the negative value. To set up the negative equation, rewrite the equation without the absolute value bars, and take the negative value of the number on the other side of the equation. For example, the negative equation for | 6 x − 2 | = 4 {\displaystyle |6x-2|=4} |6x-2|=4 is 6 x − 2 = − 4 {\displaystyle 6x-2=-4} 6x-2=-4.
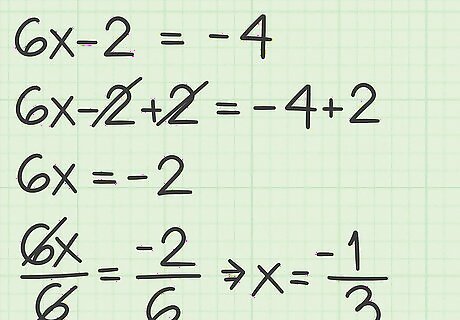
Solve the negative equation. Use algebra to solve for the variable as you would for any other equation. The result will be your second possible solution to the equation. For example: 6 x − 2 = − 4 {\displaystyle 6x-2=-4} 6x-2=-4 6 x − 2 + 2 = − 4 + 2 {\displaystyle 6x-2+2=-4+2} 6x-2+2=-4+2 6 x = − 2 {\displaystyle 6x=-2} 6x=-2 6 x 6 = − 2 6 {\displaystyle {\frac {6x}{6}}={\frac {-2}{6}}} {\frac {6x}{6}}={\frac {-2}{6}} x = − 1 3 {\displaystyle x={\frac {-1}{3}}} x={\frac {-1}{3}}
Check Your Work
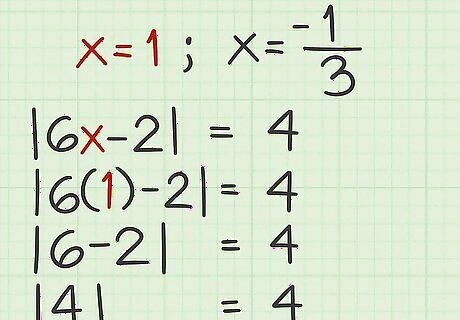
Check the result of your positive equation. You must always plug possible solutions back into the original equation to verify that they are real solutions. To check your positive equation, plug the value for x {\displaystyle x} x derived from the positive equation back into the original absolute value equation. If both sides of the equation are equal, the solution is true. For example, if the solution to the positive equation was x = 1 {\displaystyle x=1} x=1, plug 1 {\displaystyle 1} 1 into the original equation and solve: | 6 x − 2 | = 4 {\displaystyle |6x-2|=4} |6x-2|=4 | 6 ( 1 ) − 2 | = 4 {\displaystyle |6(1)-2|=4} |6(1)-2|=4 | 6 − 2 | = 4 {\displaystyle |6-2|=4} |6-2|=4 | 4 | = 4 {\displaystyle |4|=4} |4|=4

Check the result of your negative equation. Just because one solution is true, it does not mean that both are true. You must also plug the solution from the negative equation back into the original equation to verify it is a real solution. For example, if the solution to the negative equation was x = − 1 3 {\displaystyle x={\frac {-1}{3}}} x={\frac {-1}{3}}, plug − 1 3 {\displaystyle {\frac {-1}{3}}} {\frac {-1}{3}} into the original equation and solve: | 6 x − 2 | = 4 {\displaystyle |6x-2|=4} |6x-2|=4 | 6 ( − 1 3 ) − 2 | = 4 {\displaystyle |6({\frac {-1}{3}})-2|=4} |6({\frac {-1}{3}})-2|=4 | − 2 − 2 | = 4 {\displaystyle |-2-2|=4} |-2-2|=4 | − 4 | = 4 {\displaystyle |-4|=4} |-4|=4
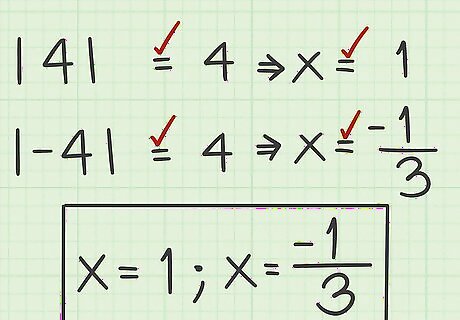
Note your valid solutions. A solution is valid if, after plugging it back into the original equation, it yields a true equation. It is possible to have two valid solutions, but you may have one solution, or no solution. For example, since | 4 | = 4 {\displaystyle |4|=4} |4|=4 and | − 4 | = 4 {\displaystyle |-4|=4} |-4|=4 are both true, then both solutions to the equation are valid. So, | 6 x − 2 | + 3 = 7 {\displaystyle |6x-2|+3=7} |6x-2|+3=7 has two possible solutions: x = 1 {\displaystyle x=1} x=1, x = − 1 3 {\displaystyle x={\frac {-1}{3}}} x={\frac {-1}{3}}.



















Comments
0 comment